题目内容
【题目】寒冬来临，豆丝飘香，豆丝是鄂州民间传统美食；某企业接到一批豆丝生产任务，约定这批豆丝的出厂价为每千克4元，按要求在20天内完成．为了按时完成任务，该企业招收了新工人，新工人李明第1天生产100千克豆丝，由于不断熟练，以后每天都比前一天多生产20千克豆丝；设李明第x天（
，且x为整数）生产y千克豆丝，解答下列问题：
(1)求y与x的关系式，并求出李明第几天生产豆丝280千克？
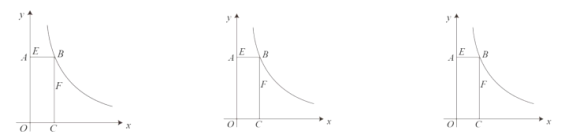
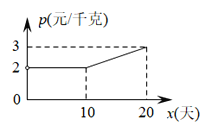
(2)设第x天生产的每千克豆丝的成本是p元，p与x之间满足如图所示的函数关系；若李明第x天创造的利润为w元，求w与x之间的函数表达式，并求出第几天的利润最大？最大利润是多少元？（利润=出厂价-成本）
【答案】（1）
，第10天生产豆丝280千克；（2）当x=13时，w有最大值，最大值为578.
【解析】
（1）根据题意可得关系式为：y=20x+80，把y=280代入y=20x+80，解方程即可求得；
（2）根据图象求得成本p与x之间的关系，然后根据利润等于订购价减去成本价，然后整理即可得到W与x的关系式，再根据一次函数的增减性和二次函数的增减性解答；
解：（1）依题意得： 
令
，则
，解得
答：第10天生产豆丝280千克.
(2) 由图象得，当0＜x＜10时，p=2；
当10≤x≤20时，设P=kx+b，
把点（10，2），（20，3）代入得，
解得
∴p=0.1x+1，
①1≤x≤10时，w=（4-2）×（20x+80）=40x+160，
∵x是整数，
∴当x=10时，w最大=560（元）；
②10＜x≤20时，w=（4-0.1x-1）×（20x+80）
=-2x2+52x+240，
=-2（x-13）2+578，
∵a=-2＜0，
∴当x=-=13时，w最大=578（元）
综上，当x=13时，w有最大值，最大值为578．
