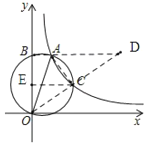
题目内容
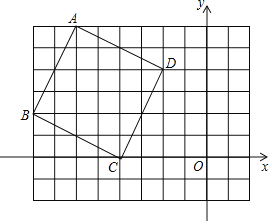
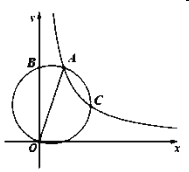
【题目】如图,点![]() 在反比例函数
在反比例函数![]() 上,以线段
上,以线段![]() 为直径的圆交该双曲线于点
为直径的圆交该双曲线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若弧
,若弧![]() 弧
弧![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.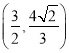 D.
D.![]()
【答案】B
【解析】
连接OC并延长OC,BA交点为D,作CE⊥OB,连接AC,设A(a,b) 则ab=2![]() ,AO=
,AO=![]() .由AO为直径可证得∠BOC=∠CAD,由
.由AO为直径可证得∠BOC=∠CAD,由![]() 可得∠BOC=∠OAC则∠OAC=∠DAC,可证△AOC≌△ACD,所以AO=AD,OC=CD,由垂径定理得BE=OE=
可得∠BOC=∠OAC则∠OAC=∠DAC,可证△AOC≌△ACD,所以AO=AD,OC=CD,由垂径定理得BE=OE=![]() ,由中位线定理可得EC=
,由中位线定理可得EC=![]() BD,最后由S△ABO=S△ECO,用a,b表示面积,可得a,b 的关系式,代入ab=2
BD,最后由S△ABO=S△ECO,用a,b表示面积,可得a,b 的关系式,代入ab=2![]() ,可得a,b的值.
,可得a,b的值.
如图:连接OC并延长OC,BA交点为D,作CE⊥OB,连接AC
设A(a,b) 则ab=2![]()
∵AB是直径
∴∠ABO=90°=∠ACO
∴AB=a,OB=b
∴AO=![]()
∵ABOC是圆的内接四边形
∴∠BOC=∠DAC
∵![]()
∴∠BOC=∠OAC
∴∠OAC=∠DAC,且AC=AC,∠ACO=∠ACD=90°
∴△AOC≌△ACD
∴AO=AD=![]() ,OC=CD
,OC=CD
∵CE⊥OB,![]()
∴OE=BE=![]() ,且OC=CD
,且OC=CD
∴EC∥BD,EC=![]() BD=
BD=![]()
∵S△ABO=S△EOC=![]()
∴![]() ab=
ab=![]() ×
×![]() ×(
×(![]() )
)
解得3a=![]()
∴b=2![]() 且ab=2
且ab=2![]()
∴a=1,b=2![]()
∴A![]() ,
,
故选B.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元。根据市场需求,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元,设每天安排![]() 人生产乙产品。
人生产乙产品。
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | — | — | 15 |
乙 |
|
| — |
(2)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等,已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润![]() (元)的最大值及相应的
(元)的最大值及相应的![]() 值。
值。