��Ŀ����
����Ŀ�����ݶ���������ص��г���۵��У�Ԥ�ƽ����ļ����ijһ��ʱ�䣬ij�����г��ڵļ����߲˵���������y1��ǧԪ���������x���֣�֮��ĺ���![]() ��ͼ����ͼ����ʾ�������߲˵���������y2��ǧԪ���������x���֣�֮��ĺ���
��ͼ����ͼ����ʾ�������߲˵���������y2��ǧԪ���������x���֣�֮��ĺ���![]() ��ͼ����ͼ����ʾ.
��ͼ����ͼ����ʾ.

��1���ֱ����y1��y2��x֮��ĺ�����ϵʽ��
��2��������г������ס��������߲˹�10�֣��������߲˵Ľ�����Ϊt�֣�д���������߲�����õ���������֮��W��ǧԪ����t���֣�֮��ĺ�����ϵʽ��������������߲˸������ٶ�ʱ ��õ���������֮�������������Ƕ��٣�
���𰸡�. �⣺��1��![]() . ������������������������������1��
. ������������������������������1��
![]() .��������������������������3��
.��������������������������3��
��2��![]() ��
��
![]() .������������������������4��
.������������������������4��
��![]() .
.
���Լ����߲˽�����Ϊ6�֣������߲˽�����Ϊ4��ʱ����õ���������֮��������������9200Ԫ. ��������������6��
��������
���⣨1���ѣ�5��3�����������������������k��ֵҲ�������![]() �Ĺ�ϵʽ����ԭ������1��2������5��6�����뼴�����
�Ĺ�ϵʽ����ԭ������1��2������5��6�����뼴�����![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��2����������֮��W=�����߲˵�����+�����߲˵����������䷽����ö��κ�������ֵ���ɣ�
���������
��1��������ã�5k=3��
���k=0��6��
��![]() =0��6x��
=0��6x��
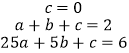
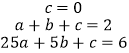 ��
��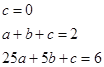 ����ã�
����ã�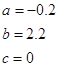
��![]() ��
��
��2��W=0��6��10-t��+��-0��2![]() +2��2t��=-0��2t2+1��6t+6=-0��2��t-4��2+9��2
+2��2t��=-0��2t2+1��6t+6=-0��2��t-4��2+9��2
���Լ����߲˽�����Ϊ6�֣������߲˽�����Ϊ4�֣���õ���������֮��������������9200Ԫ��