题目内容
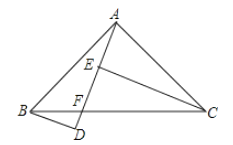
【题目】如图,线段AB=8cm,射线AN⊥AB,垂足为点A,点C是射线上一动点,分别以AC,BC为直角边作等腰直角三角形,得△ACD与△BCE,连接DE交射线AN于点M,则CM的长为__________.
【答案】4cm.
【解析】
过点E作EF⊥AN于F,先利用AAS证出△ABC≌△FCE,从而得出AB=FC=8cm,AC=FE,然后利用AAS证出△DCM≌△EFM,从而求出CM的长.
解:过点E作EF⊥AN于F,如图所示
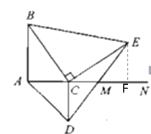
∵AN⊥AB,△BCE和△ACD为等腰直角三角形,
∴∠BAC=∠BCE=∠ACD=∠CFE =90°,BC=CE,AC=CD
∴∠ABC+∠ACB=90°,∠FCE+∠ACB =90°,
∴∠ABC =∠FCE,
在△ABC和△FCE中
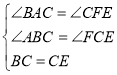
∴△ABC≌△FCE
∴AB=FC=8cm,AC=FE
∴CD= FE
在△DCM和△EFM中
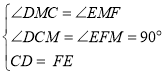
∴△DCM≌△EFM
∴CM=FM=![]() FC=4cm.
FC=4cm.
故答案为:4cm.

练习册系列答案
相关题目