题目内容
【题目】平面直角坐标系中,A、O两点的坐标分别为(2,0),(0,0),点P在正比例函数y=x(x>0)图象上运动,则满足△PAO为等腰三角形的P点的坐标为_____.
【答案】(1,1)或(![]() ,
,![]() )或(2,2)
)或(2,2)
【解析】
分OP=AP、OP=OA、AO=AP三种情况考虑:①当OP1=AP1时,△AOP1为等腰直角三角形,根据等腰直角三角形的性质结合点A的坐标可得出点P1的坐标;②当OP2=OA时,过点P2作P2B⊥x轴,则△OBP2为等腰直角三角形,根据等腰直角三角形的性质结合点A的坐标可得出点P2的坐标;③当AO=AP3时,△OAP3为等腰直角三角形,根据等腰直角三角形的性质结合点A的坐标可得出点P3的坐标.综上即可得出结论
∵点A的坐标为(2,0),
∴OA=2.
分三种情况考虑,如图所示.
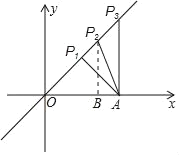
①当OP1=AP1时,∵∠AOP1=45°,
∴△AOP1为等腰直角三角形.
又∵OA=2,
∴点P1的坐标为(1,1);
②当OP2=OA时,过点P2作P2B⊥x轴,则△OBP2为等腰直角三角形.
∵OP2=OA=2,
∴OB=BP2=![]() ,
,
∴点P2的坐标为(![]() ,
,![]() );
);
③当AO=AP3时,△OAP3为等腰直角三角形.
∵OA=2,
∴AP3=OA=2,
∴点P3的坐标为(2,2).
综上所述:点P的坐标为(1,1)或(![]() ,
,![]() )或(2,2).
)或(2,2).
故答案为:(1,1)或(![]() ,
,![]() )或(2,2).
)或(2,2).

练习册系列答案
相关题目
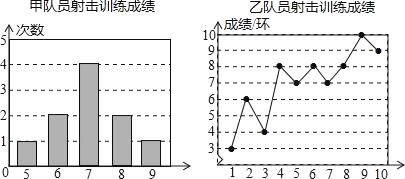
【题目】甲、乙两名队员参加射击训练(各射击10次),成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下表:
平均成绩/环 | 中位数/环 | 众数/环 | 方差/环2 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)求出表格中a,b,c的值;
(2)分别运用表中的统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?