题目内容
【题目】(1)操作发现:
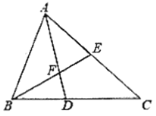
如图①,在![]() 中,
中,![]() ,点D是BC上一点,沿AD折叠
,点D是BC上一点,沿AD折叠![]() ,使得点C恰好落在AB上的点E处.请写出AB、AC、CD之间的关系________________________________;
,使得点C恰好落在AB上的点E处.请写出AB、AC、CD之间的关系________________________________;
(2)问题解决:
如图②,若(1)中![]() ;
;![]() ,其他条件不变,请猜想AB、AC、CD之间的关系,并证明你的结论;
,其他条件不变,请猜想AB、AC、CD之间的关系,并证明你的结论;
(3)类比探究:
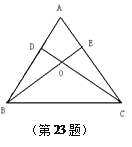
如图③,在四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,连接AC、点E是CD上一点,沿AE折叠,使得点D正好落在AC上的F处,若
,连接AC、点E是CD上一点,沿AE折叠,使得点D正好落在AC上的F处,若![]() ,求DE的长.
,求DE的长.

【答案】解:(1)![]() ;(2)
;(2)![]() ,证明详见解析;(3)
,证明详见解析;(3)![]() .
.
【解析】
(1)由翻折的性质得到AE=AC,DE=DC,然后证明△BED为等腰直角三角形,从而得到BE=ED ,故可证明得AB=AC+CD;
(2)由翻折的性质得到AE=AC,DE=DC,∠C=∠AED,由三角形外角的性质可证明∠B=∠AED由三角形外角的性质可证明![]() ,从而得到BE=ED于是可证明AB-AC+CD;
,从而得到BE=ED于是可证明AB-AC+CD;
(3)过点B作BH⊥AC,垂足为H,由特殊锐角三角函数值可知CH的长,然后求得AD的长,最后根据AC=AD+DE求解即可.
解:(1)
![]() 90°
90°
∴![]() 45°
45°
由翻折的性质得到AE=AC,DE=DC,![]() 90°
90°
∴![]() =45°
=45°
∴BE=ED
∴BE=DC
∴![]() ;
;
(2)连接DE,有题意可知:
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]() .
.
(3)作BH⊥AC于点H,根据∠B=120°, AB=BC,∴∠BAC=∠BCA=30°

在Rt△BHC中,CH=BC×![]() =
=![]()
∵AH=CH,
∴AC=2CH=2(![]() )
)
∵AD=DC, ∠D=90°
∴∠ACD=45°,在Rt△ACD中,根据勾股定理有![]()
∴AD2=2(![]() )2
)2
∴AD=![]()
又由(1),(2)可知,AD+ED=AC
∴DE=AC-AD=2![]() +2
+2![]() -(2
-(2![]() +6)=
+6)=![]()

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目