题目内容
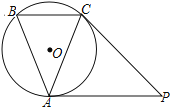
【题目】已知如图,点 C 在以 AB 为直径的⊙O 上,点 D 在 AB 的延长线上,∠BCD =∠A.
(1)求证:CD 为⊙O 的切线;
(2)过点 C 作 CE⊥AB 于点 E.若 CE = 2,cos D =![]() ,求 AD 的长.
,求 AD 的长.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)先连接CO,根据AB是⊙O直径,得出∠1+∠OCB=90°,再根据AO=CO,得出∠1=∠A,最后根据∠4=∠A,证出OC⊥CD,即可得出CD为⊙O的切线;
(2)根据OC⊥CD,得出∠3+∠D=90°,再根据CE⊥AB,得出∠3+∠2=90°,从而得出cos∠2=cosD,再在△OCE中根据余弦定义得出CO的值,根据勾股定理求出OE的值,利用sinD=sin∠2,求出OD的值,即可得出AD的长.
试题解析:证明:(1)连接CO.∵AB是⊙O直径,∴∠1+∠OCB=90°.∵AO=CO,∴∠1=∠A.∵∠4=∠A,∴∠4+∠OCB=90°.即∠OCD=90°,∴OC⊥CD.又∵OC是⊙O半径,∴CD为⊙O的切线.
(2)∵OC⊥CD于C,∴∠3+∠D=90°.∵CE⊥AB于E,∴∠3+∠2=90°,∴∠2=∠D,∴cos∠2=cosD.在△OCE中,∠OCD=90°,∴cos∠2=![]() .∵cosD=
.∵cosD=![]() ,CE=2,∴
,CE=2,∴![]() ,∴CO=
,∴CO=![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() ,∴OE=
,∴OE=![]() =
= =
=![]() .∵sinD=sin∠2,
.∵sinD=sin∠2,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,解得:OD=
,解得:OD= ![]() ,AD=OD+OA=
,AD=OD+OA=![]() =
=![]() .
.


【题目】观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此解答下面的问题
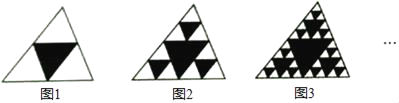
(1)填写下表:
图形 | 挖去三角形的个数 |
图形1 | 1 |
图形2 | 1+3 |
图形3 | 1+3+9 |
图形4 |
|
(2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)
(3)若图n+1中挖去三角形的个数为wn+1,求wn+1﹣Wn