Question

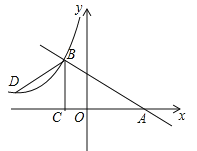
【题目】如图，在平面直角坐标系中，抛物线y=-x2+bx+c经过点（0，6），其对称轴为直线x=．在x轴上方作平行于x轴的直线l与抛物线交于A、B两点（点A在对称轴的右侧），过点A、B作x轴的垂线，垂足分别为D、C．设A点的横坐标为m．

（1）求此抛物线所对应的函数关系式．

（2）当m为何值时，矩形ABCD为正方形．

（3）当m为何值时，矩形ABCD的周长最大，并求出这个最大值．

Answer 1

【答案】（1）y=-x2+3x+6；（2）；（3）当时，矩形ABCD的周长最大为．

【解析】

（1）首先根据对称轴求得b值，然后代入点（0，6）求得c值即可；
（2）首先用含m的代数式表示出线段AB、AD的长，然后利用正方形ABCD的AB=CD得到有关m的等式求得m的值即可；
（3）表示出正方形的周长，然后利用配方法求最值即可；

（1）∵对称轴为直线x=，

∴，

∴b=3．

把（0，6）代入y=-x2+3x+c得，

6=-0+3×0+c，

解得c=6．

∴此抛物线所对应的函数关系式为y=-x2+3x+6．

（2）根据题意，得

AD=-m2+3m+6．

∵矩形ABCD为正方形，AB=AD．

∴2m-3=-m2+3m+6，

解得．

∵点A在对称轴的右侧，

∴．

∴（舍去）．

∴．

（3）设矩形ABCD的周长为C．

．

∴当时，矩形ABCD的周长最大为．