题目内容
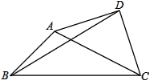
【题目】如图,△ABC中,D是边BC的中点,E是AB边上一点,且AD⊥CE于O,AD=AC=CE.
(1)求证:∠B=45°;
(2)求![]() 的值;
的值;
(3)直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)作AF⊥BC于F,由等腰三角形的性质得出DF=CF,∠ADC=∠ACD,∠CEA=∠EAC,证出∠1=∠2,∠B=∠EAF,即可得出结论;
(2)设DF=CF=m,则BC=4m,AF=BF=3m,由勾股定理得:CE=AD=![]() m,由三角形面积公式先得出AD×OC=CD×AF,求出OC=
m,由三角形面积公式先得出AD×OC=CD×AF,求出OC=![]() m,得出OE=CE﹣OC=
m,得出OE=CE﹣OC=![]() m,即可得出结果;
m,即可得出结果;
(3)作EG⊥BC于G,则△BEG是等腰直角三角形,得出EG=BG,设EG=BG=x,则CG=4m﹣x,在Rt△CEG中,由勾股定理得出方程,解方程得出EG=m,BE=![]() m,即可得出结果.
m,即可得出结果.
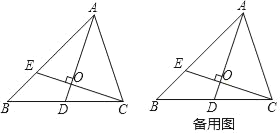
(1)证明:作AF⊥BC于F,如图1所示:
∵AD=AC=CE,
∴DF=CF,∠ADC=∠ACD,∠CEA=∠EAC,
∵∠1+∠ADC=90°,∠ACD+∠2=90°,
∴∠1=∠2,
∵∠B+∠1=∠CEA=∠EAC=∠EAF+∠2,
∴∠B=∠EAF,
∵∠B+∠EAF=90°,
∴∠B=∠EAF=45°;
(2)解:设DF=CF=m,则BC=4m,AF=BF=3m,
由勾股定理得:CE=AD=![]() m,
m,
∵△ACD的面积=![]() AD×OC=
AD×OC=![]() CD×AF,
CD×AF,
∴AD×OC=CD×AF,
即OC×![]() m=2m×3m,
m=2m×3m,
∴OC=![]() m,
m,
∴OE=CE﹣OC=![]() m﹣
m﹣![]() m=
m=![]() m,
m,
∴![]() =
=![]() ;
;
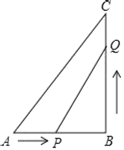
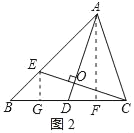
(3)解:作EG⊥BC于G,如图2所示:
则△BEG是等腰直角三角形,
∴EG=BG,
设EG=BG=x,则CG=4m﹣x,
在Rt△CEG中,由勾股定理得:x2+(4m﹣x)2=(![]() m)2,
m)2,
解得:x=m,或x=3m(舍去),
∴EG=m,
∴BE=![]() m,
m,
∴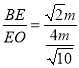 =
=![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案