题目内容
【题目】在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2﹣4ax﹣
交x轴正半轴于点A（5，0），交y轴于点B．
（1）求抛物线的解析式；
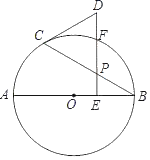
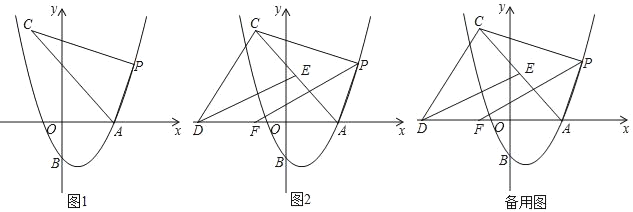
（2）如图1，点P为第一象限内抛物线上一点，连接AP，将射线AP绕点A逆时针旋转60°，与过点P且垂直于AP的直线交于点C，设点P横坐标为t，点C的横坐标为m，求m与t之间的函数关系式（不要求写出t的取值范围）；
（3）如图2，在（2）的条件下，过点C作直线交x轴于点D，在x轴上取点F，连接FP，点E为AC的中点，连接ED，若F的横坐标为-
，∠AFP＝∠CDE，且∠FAP+∠ACD＝180°，求m的值．
【答案】（1）y＝
x2﹣
x﹣
（2）m＝
t2+
t+3（3）-
【解析】
（1）把点A坐标代入即能求a的值．
（2）由AP⊥PC和旋转60°得∠PAC=60°得到特殊Rt△APC．利用已知点P、C的横坐标的条件，分别过点C、点P作坐标轴的垂线，构造三垂直模型下的相似，且相似比即为PC与AP的比．用t、m表示相似三角形对应边的长度，利用相似比为列方程，即得到m与t的关系式．
（3）由特殊Rt△APC中∠ACP=30°与点E为AC的中点的条件得到CE=AE=AP；构造PQ=AP（Q在x轴上）得∠PAQ=∠PQA，再由∠FAP+∠ACD=180°和∠FAP邻补角为∠PAN得到∠ACD=∠PAN，即得到∠ACD=∠PAQ=∠PQA，因此构造的△QFP与△CDE全等，得到QF=CD．由四边形APCD内角和为360°可求得∠CDF=60°，作CH⊥x轴构造特殊直角三角形，利用CH=MN即可以t的式子表示CH，进而用t表示CD．又易由t的式子表示QF，列方程即求得t的值．再代回（2）的式子即求出m的值．
（1）∵抛物线y＝ax2﹣4ax﹣过点A（5，0），
∴25a﹣20a﹣＝0，
解得：a＝，
∴抛物线的解析式为
；
（2）过点P作MN⊥x轴于点N，过点C作CM⊥MN于点M，
∴∠M＝∠ANP＝90°，
∴∠MCP+∠CPM＝90°.
∵CP⊥AP，
∴∠APC＝90°，
∴∠CPM+∠APN＝90°，
∴∠MCP＝∠APN，
∴△MCP∽△NPA，
∴
，
∵∠APC＝90°，∠PAC＝60°，
∴∠ACP＝30°，tan∠PAC＝
，
∴
，即
.
∵xP＝t，xC＝m，
∴MC＝t﹣m，PN＝yP＝
，
∴t﹣m＝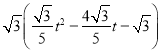
，
整理得：m＝
，
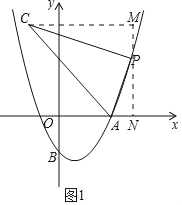
（3）过点C作CH⊥x轴于点H，在x轴上取点Q，连接PQ且使PQ＝AQ，
∴∠CHD＝90°，∠PAN＝∠PQN，
∵∠ACP＝30°，∠APC＝90°，点E是AC中点，
∴AP＝
AC＝CE＝AE，
∴CE＝PQ，
∵∠FAP+∠ACD＝180°，∠FAP+∠PAN＝180°，
∴∠ACD＝∠PAN，
∴∠ACD＝∠PQN，
在△CDE与△QFP中
，
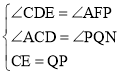∴△CDE≌△QFP（AAS），
∴CD＝QF，
由（1）得，AN＝t﹣5，PM＝
，PN＝，
∴CH＝MN＝PM+PN＝
＝
.
∵∠CDH＝360°﹣∠CDP﹣∠APC﹣∠FAP＝360°﹣（∠ACD+∠FAP）﹣∠ACP﹣∠APC＝360°﹣180°﹣30°﹣90°＝60°，
∴sin∠CDH＝
，
∴CD＝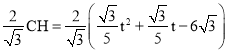
＝
，
∵F（﹣
，0），
∴QF＝AF+AQ＝AF+2AN＝5﹣（﹣）+2（t﹣5）＝2t﹣
，
∴
，
解得：t1＝﹣3，t2＝7，
∵点P在第一象限，t＞5，
∴t＝7，
∴m＝
.
