题目内容
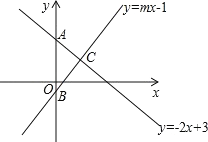
【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1…按这样的规律进行下去,第2018个正方形的面积为( )

A. 20×(![]() )2017 B. 20×(
)2017 B. 20×(![]() )2018 C. 20×(
)2018 C. 20×(![]() )4036 D. 20×(
)4036 D. 20×(![]() )4034
)4034
【答案】D
【解析】
根据勾股定理求得AB=AD=BC=![]() ,再根据两对对应角相等的三角形相似,证明△ABA1∽△DOA,根据相似三角形对应边成比例可以得到AB=2A1B,所以正方形A1B1C1C的边长等于正方形ABCD边长的
,再根据两对对应角相等的三角形相似,证明△ABA1∽△DOA,根据相似三角形对应边成比例可以得到AB=2A1B,所以正方形A1B1C1C的边长等于正方形ABCD边长的![]() ,以此类推,后一个正方形的边长是前一个正方形的边长的
,以此类推,后一个正方形的边长是前一个正方形的边长的![]() ,然后即可求出第2018个正方形的边长与第1个正方形的边长的关系,从而求出第2018个正方形的面积.
,然后即可求出第2018个正方形的边长与第1个正方形的边长的关系,从而求出第2018个正方形的面积.
∵点A的坐标为(2,0),点D的坐标为(0,4),
∴OA=2,OD=4
∵∠AOD=90°,
∴AB=AD=BC=![]() ,∠ODA+∠OAD=90°,
,∠ODA+∠OAD=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,
∴∠ABA1=90°,∠OAD+∠BAA1=90°,
∴∠ODA=∠BAA1,
∴△ABA1∽△DOA,
∴OD:AO=AB:A1B=2,
∴BC=2A1B,
∴A1C=![]() BC,
BC,
以此类推A2C1= ![]() A1C,A3C2=
A1C,A3C2=![]() A2C1,…,
A2C1,…,
即后一个正方形的边长是前一个正方形的边长的![]() 倍,
倍,
∴第2018个正方形的边长为(![]() )2017BC,
)2017BC,
∴正方形A2018B2018C2018C2017,即第2018个正方形的面积为[(![]() )2017BC]2=20×(
)2017BC]2=20×(![]() )4034.
)4034.
故选D.

练习册系列答案
相关题目