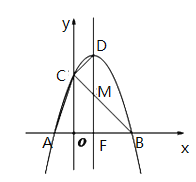题目内容
【题目】问题探究:
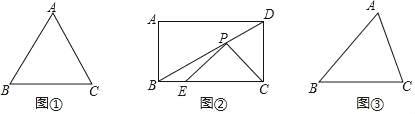
(1)如图①,已知等边△ABC,边长为4,则△ABC的外接圆的半径长为 .
(2)如图②,在矩形ABCD中,AB=4,对角线BD与边BC的夹角为30°,点E在为边BC上且BE=![]() BC,点P是对角线BD上的一个动点,连接PE,PC,求△PEC周长的最小值.
BC,点P是对角线BD上的一个动点,连接PE,PC,求△PEC周长的最小值.
问题解决:
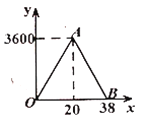
(3)为了迎接新年的到来,西安城墙举办了迎新年大型灯光秀表演.其中一个镭射灯距城墙30米,镭射灯发出的两根彩色光线夹角为60°,如图③,若将两根光线(AB,AC)和光线与城墙的两交点的连接的线段(BC)看作一个三角形,记为△ABC,那么该三角形周长有没有最小值?若有,求出最小值,若没有,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)△ABC的周长最小值为60
;(3)△ABC的周长最小值为60![]() .
.
【解析】
(1)作△ABC外接圆,作直径AD,连接BD,根据等边三角形性质求出∠C=60°,根据圆周角定理求出∠D=∠C=60°,解直角三角形求出AD即可.
(2)△PEC周长的最小实质是PE+PC,转化为将军饮马模型求出P点,然后利用勾股定理即可求出E′C即可解答,
(3)先由定角定高可知BC的最小值为三角形是等腰三角形AB=AC时,BC最小,而求AB+AC,可以先将A点沿BC方向平移BC,构造平行四边形将AB转化为长,则AB+AC最小转化为AC+CD最小,作A点对称点A′,连接A′D,与BC交点与C重合,此时BC、AB+AC同时取最小值,即可知三角形周长有没有最小值.
解:(1)如图,作三角形外接圆⊙O,作直径AD,连接BD,
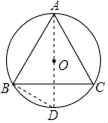
∵等边△ABC内接于⊙O,AD为直径,
∴∠C=60°=∠D,∠ABD=90°,
∵sin∠D=![]() ,
,
∴AD=![]()
∴⊙0的半径是![]() .
.
故答案为![]() ;
;
(2)如图2,作点E关于BD的对称点E′,连接E′C交BD于P,连接PE,此时△PEC周长周长最小.

连接BE′,过E′作E′H⊥BC,
∵∠DBC=30°,AB=CD=4,
∴BC=4![]() ,
,
又∵BE=![]() BC.
BC.
∴BE=![]()
∵点E′是关于BD的对称点E
∴∠EBH=60°,BE′=BE=![]() ,
,
∴BH=![]() ,E′H=
,E′H=![]() ,
,
∴HC=![]() ,
,
∴E′C=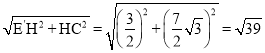
∵△PEC周长=PC+PE+EC=PE′+EC=![]()
(3)如图3,∵∠BAC=60°,AH=30米,
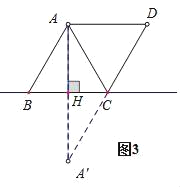
∴当AB=AC时,边BC取最小值,
∴此时BC=AC=20![]() ,
,
作ABCD,作A点关于直线BC的对称点A′,连接A′D,AB+AC=CD+A′C,
当A′,C,D在一条直线上时,AB+AC最小,
此时,△ABC应为等边三角形,AB+AC=![]()
∵AB+AC和BC的最小值能够同时取到,
故△ABC的周长最小值为![]() .
.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案