题目内容
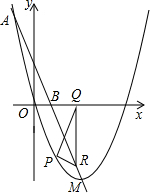
如图,已知抛物线的顶点为M(2,-4),且过点A(-1,5),连接AM交x轴于点B.
(1)求这条抛物线的解析式;
(2)求点B的坐标;
(3)设点P(x,y)是抛物线在x轴下方、顶点左方一段上的动点,连接PO,以P为顶点、PO为腰的等腰三角形的另一顶点Q在x轴的垂线交直线AM于点R,连接PR,设△PQR的面积为S,求S与x之间的函数关系式;
(4)在上述动点P(x,y)中,是否存在使S△PQR=2的点?若存在,求点P的坐标;若不存在,说明理由.
(1)求这条抛物线的解析式;
(2)求点B的坐标;
(3)设点P(x,y)是抛物线在x轴下方、顶点左方一段上的动点,连接PO,以P为顶点、PO为腰的等腰三角形的另一顶点Q在x轴的垂线交直线AM于点R,连接PR,设△PQR的面积为S,求S与x之间的函数关系式;
(4)在上述动点P(x,y)中,是否存在使S△PQR=2的点?若存在,求点P的坐标;若不存在,说明理由.

(1)∵根据抛物线过M(2,-4),A(-1,5),O(0,0)三点,
设抛物线的解析式为y=ax2+bx(a≠0),
把M(2,-4),A(-1,5)代入得
,
解得
,
这条抛物线的解析式为y=x2-4x;
(2)设直线AM的解析式为y=kx+b(k≠0),
把M(2,-4),A(-1,5)两点代入得
,
解得
,
故直线AM的解析式为y=-3x+2,
令y=0,解得x=
,
故B点坐标为(
,0);

(3)设点P(x,y)则,Q的坐标是(2x,0),
代入直线AM的解析式y=-3x+2,就可以求出R的坐标.
得到QR的长度,QR边上的高是x,
∴S=
.
(4)s=2代入(3)中函数的解析式即可得
2=-3x2+x或2=3x2-x,
当2=-3x2+x,方程的△<0,方程无解;
当2=3x2-x,解得:x1=1,x2=-
,
当x=1时y=x2-4x=-3,即抛物线上的P点坐标为(1,-3)时,s=2成立;
当x=-
<0(舍去),
∴存在动点P,使S=2,此时P点坐标为(1,-3).
设抛物线的解析式为y=ax2+bx(a≠0),
把M(2,-4),A(-1,5)代入得
|
解得
|
这条抛物线的解析式为y=x2-4x;
(2)设直线AM的解析式为y=kx+b(k≠0),
把M(2,-4),A(-1,5)两点代入得
|
解得
|
故直线AM的解析式为y=-3x+2,
令y=0,解得x=
| 2 |
| 3 |
故B点坐标为(
| 2 |
| 3 |

(3)设点P(x,y)则,Q的坐标是(2x,0),
代入直线AM的解析式y=-3x+2,就可以求出R的坐标.
得到QR的长度,QR边上的高是x,
∴S=
|
(4)s=2代入(3)中函数的解析式即可得
2=-3x2+x或2=3x2-x,
当2=-3x2+x,方程的△<0,方程无解;
当2=3x2-x,解得:x1=1,x2=-
| 2 |
| 3 |
当x=1时y=x2-4x=-3,即抛物线上的P点坐标为(1,-3)时,s=2成立;
当x=-
| 2 |
| 3 |
∴存在动点P,使S=2,此时P点坐标为(1,-3).

练习册系列答案
相关题目

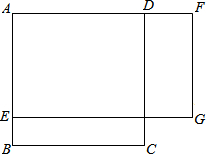
 绕点A逆时针旋转,使点B落在y轴的E点上,则C和D点依次落在第二象限的F点上和x轴的G点上(如图).
绕点A逆时针旋转,使点B落在y轴的E点上,则C和D点依次落在第二象限的F点上和x轴的G点上(如图).
 单位长度,平移中四边形BCFE与△AEF重叠的面积为S.
单位长度,平移中四边形BCFE与△AEF重叠的面积为S.