Question

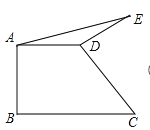
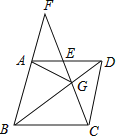
【题目】如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E．

（1）求证：AG=CG；

（2）求证：AG2=GE·GF．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）根据菱形的性质得到AB∥CD，AD=CD，∠ADB=∠CDB，推出△ADG≌△CDG，根据全等三角形的性质即可得到结论；
（2）由全等三角形的性质得到∠EAG=∠DCG，等量代换得到∠EAG=∠F，求得△AEG∽△FGA，即可得到结论．

解：（1）∵四边形ABCD是菱形，
∴AB∥CD，AD=CD，∠ADB=∠CDB，
在△ADG与△CDG中， ,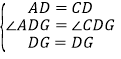

∴△ADG≌△CDG（SAS），
∴AG=CG；

（2）∵△ADG≌△CDG，AB∥CD
∴∠F=∠FCD，∠EAG=∠GCD，
∴∠EAG=∠F
∵∠AGE=∠AGE，
∴△AEG∽△FAG，

∴ ,

∴AG2=GEGF．