��Ŀ����
����Ŀ���ţ�1������ѧ��ȤС�龭���г����飬������ij����Ʒ�ڵ�x��1��x��90������ۼ����������������Ϣ���±���
ʱ��x���죩 | 1��x��50 | 50��x��90 |
�ۼۣ�Ԫ/���� | x+40 | 90 |
ÿ������������ | 200��2x | 200��2x |
��֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒ��ÿ������ΪyԪ
��1�����y��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������4800Ԫ����ֱ��д�������
���𰸡���1��y��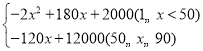 ����2��45��ʱ�����������6050Ԫ����3��41�죮
����2��45��ʱ�����������6050Ԫ����3��41�죮
��������
��1�����ݵ��۳����������ɵ����ɵ�y��x�ĺ�����ϵʽ��
��2�����ݷֶκ��������ʣ��ɷֱ�ó����ֵ�������������ıȽϣ��ɵô𰸣�
��3�����ݶ��κ���ֵ���ڻ����4800��һ�κ���ֵ���ڻ����48000���ɵò���ʽ�����ݽⲻ��ʽ�飬�ɵô𰸣�
�⣺��1����1��x��50ʱ��y����200��2x����x+40��30������2x2+180x+2000��
��50��x��90ʱ��
y����200��2x����90��30������120x+12000��
����������y��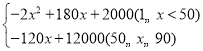 ��
��
��2����1��x��50ʱ��
y����2x2+180x+2000��
y����2��x��45��2+6050��
��a����2��0��
����κ��������£����κ����Գ���Ϊx��45��
��x��45ʱ��y���6050��
��50��x��90ʱ��y��x���������С��
��x��50ʱ��y���6000��
��������������Ʒ��45��ʱ��������������������������6050Ԫ��
��3���ٵ�1��x��50ʱ��y����2x2+180x+2000��4800��
��ã�20��x��70��
���������4800Ԫ��������20��x��50����30�죻
�ڵ�50��x��90ʱ��y����120x+12000��4800��
��ã�x��60��
���������4800Ԫ��������50��x��60����11�죬
���Ը���Ʒ���������۹����У���41��ÿ������������4800Ԫ��

 �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д� �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�