题目内容
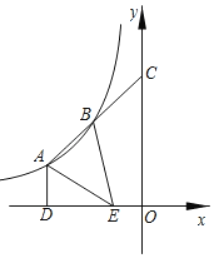
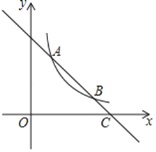
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 在第一象限的图象交于
在第一象限的图象交于![]() 和B两点,与
和B两点,与![]() 轴交于点C.
轴交于点C.
(1)求出反比例函数的解析式;
(2)若点P在![]() 轴上,且△APC的面积为5,求点P的坐标.
轴上,且△APC的面积为5,求点P的坐标.
(3)根据图象,直接写出使一次函数的值大于反比例函数的值的x的取值范围.
【答案】(1)![]() ;(2)(﹣2,0)或(8,0);(3)
;(2)(﹣2,0)或(8,0);(3)![]() .
.
【解析】
(1)先把点![]() 代入
代入![]() 中求出
中求出![]() 得到
得到![]() 然后把
然后把![]() 点坐标代入
点坐标代入![]() 中求出
中求出![]() 得到反比例函数的表达式;
得到反比例函数的表达式;
(2)先确定![]() ,设
,设![]() ,利用三角形面积公式得到
,利用三角形面积公式得到![]() ,解方程可得到
,解方程可得到![]() 的坐标;
的坐标;
(3)先解方程组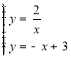 得
得![]() ,然后在第一象限内写出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.
,然后在第一象限内写出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.
解:(1)把点![]() 代入
代入![]() ,得
,得![]() ,
,
![]()
把![]() 代入反比例函数
代入反比例函数![]() ,
,
![]() ;
;
![]() 反比例函数的表达式为
反比例函数的表达式为![]() ;
;
(2)当![]() 时,
时,![]() ,解得
,解得![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,
![]() ,
,
![]() 或
或![]() ,
,
![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
(3)解方程组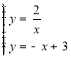 得
得![]() 或
或![]() ,
,
![]() ,
,
![]() 当
当![]() 时,一次函数的值大于反比例函数的值的
时,一次函数的值大于反比例函数的值的![]() 的取值范围为
的取值范围为![]() .
.

【题目】小颖“综合与实践”小组学习了三角函数后,开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,如表是不完整测量数据.
课题 | 测量旗杆的高度 | |||
成员 | 组长:小颖,组员:小明,小刚,小英 | |||
测量工具 | 测量角度的仪器,皮尺等 | |||
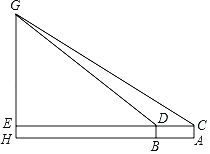
测量示意图 |
| 说明: 线段GH表示学校旗杆,测量角度的仪器的高度AC=BD=1.62m,测点A,B与H在同一水平直线上,A,B之间的距离可以直接测得,且点G,H,A,B,C,D都在同一竖直平面内,点C,D,E在同一条直线上,点E在GH上. | ||
测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 |
∠GCE的度数 | 30.6° | 31.4° | 31° | |
∠GDE的度数 | 36.8° | 37.2° | 37° | |
A,B之间的距离 | 10.1m | 10.5m | m | |
… | … | |||
(1)任务一:完成表格中两次测点A,B之间的距离的平均值.
(2)任务二:根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆GH的高度.(精确到0.1m)(参考数据:sin31°≈0.51,cos31°≈0.86,tan31°≈0.60,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)