题目内容
如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
(1)求点B的坐标;

(2)求经过点A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
(1)如图,过B点作BC⊥x轴,垂足为C,则∠BCO=90°,
∵∠AOB=120°,
∴∠BOC=60°,
又∵OA=OB=4,
∴OC=
OB=
×4=2,BC=OB•sin60°=4×
=2
,
∴点B的坐标为(-2,-2
);
(2)∵抛物线过原点O和点A、B,
∴可设抛物线解析式为y=ax2+bx,
将A(4,0),B(-2.-2
)代入,得
,
解得
,
∴此抛物线的解析式为y=-
x2+
x
(3)存在,
如图,抛物线的对称轴是直线x=2,直线x=2与x轴的交点为D,设点P的坐标为(2,y),
①若OB=OP,
则22+|y|2=42,
解得y=±2
,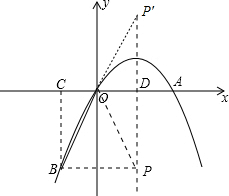
当y=2
时,在Rt△P′OD中,∠P′DO=90°,sin∠P′OD=
=
,
∴∠P′OD=60°,
∴∠P′OB=∠P′OD+∠AOB=60°+120°=180°,
即P′、O、B三点在同一直线上,
∴y=2
不符合题意,舍去,
∴点P的坐标为(2,-2
)
②若OB=PB,则42+|y+2
|2=42,
解得y=-2
,
故点P的坐标为(2,-2
),
③若OP=BP,则22+|y|2=42+|y+2
|2,
解得y=-2
,
故点P的坐标为(2,-2
),
综上所述,符合条件的点P只有一个,其坐标为(2,-2
),
∵∠AOB=120°,
∴∠BOC=60°,
又∵OA=OB=4,
∴OC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴点B的坐标为(-2,-2
| 3 |
(2)∵抛物线过原点O和点A、B,
∴可设抛物线解析式为y=ax2+bx,
将A(4,0),B(-2.-2
| 3 |
|
解得
|
∴此抛物线的解析式为y=-
| ||
| 6 |
2
| ||
| 3 |
(3)存在,
如图,抛物线的对称轴是直线x=2,直线x=2与x轴的交点为D,设点P的坐标为(2,y),
①若OB=OP,
则22+|y|2=42,
解得y=±2
| 3 |

当y=2
| 3 |
| PD |
| OP |
| ||
| 2 |
∴∠P′OD=60°,
∴∠P′OB=∠P′OD+∠AOB=60°+120°=180°,
即P′、O、B三点在同一直线上,
∴y=2
| 3 |
∴点P的坐标为(2,-2
| 3 |
②若OB=PB,则42+|y+2
| 3 |
解得y=-2
| 3 |
故点P的坐标为(2,-2
| 3 |
③若OP=BP,则22+|y|2=42+|y+2
| 3 |
解得y=-2
| 3 |
故点P的坐标为(2,-2
| 3 |
综上所述,符合条件的点P只有一个,其坐标为(2,-2
| 3 |

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
 于点B,tan∠OAB=
于点B,tan∠OAB=