题目内容
如图．已知二次函数y=-x2+bx+3的图象与x轴的一个交点为A（4，0），与y轴交于点B．
（1）求此二次函数关系式和点B的坐标；
（2）在x轴的正半轴上是否存在点P．使得△PAB是以AB为底边的等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．
（1）求此二次函数关系式和点B的坐标；
（2）在x轴的正半轴上是否存在点P．使得△PAB是以AB为底边的等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．
（1）把点A（4，0）代入二次函数有：
0=-16+4b+3
得：b=
所以二次函数的关系式为：y=-x2+
x+3．
当x=0时，y=3
∴点B的坐标为（0，3）．
（2）如图：
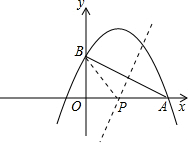作AB的垂直平分线交x轴于点P，连接BP，
则：BP=AP
设BP=AP=x，则OP=4-x，
在直角△OBP中，BP2=OB2+OP2
即：x2=32+（4-x）2
解得：x=
∴OP=4-
=
所以点P的坐标为：（
，0）
综上可得点P的坐标为（
，0）．
0=-16+4b+3
得：b=
| 13 |
| 4 |
所以二次函数的关系式为：y=-x2+
| 13 |
| 4 |
当x=0时，y=3
∴点B的坐标为（0，3）．
（2）如图：
作AB的垂直平分线交x轴于点P，连接BP，则：BP=AP
设BP=AP=x，则OP=4-x，
在直角△OBP中，BP2=OB2+OP2
即：x2=32+（4-x）2
解得：x=
| 25 |
| 8 |
∴OP=4-
| 25 |
| 8 |
| 7 |
| 8 |
所以点P的坐标为：（
| 7 |
| 8 |
综上可得点P的坐标为（
| 7 |
| 8 |
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
，OB=4，现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD，已知一抛物线经过C、D、B三点．
