题目内容
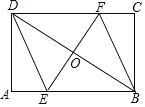
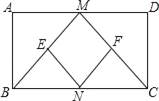
【题目】如图，在矩形ABCD中，M，N分别是AD，BC的中点，E，F分别是线段BM，CM的中点，若AB=8，AD=12，则四边形ENFM的周长是多少？
【答案】20
【解析】分析：根据M是边AD的中点，得AM=DM=6，根据勾股定理得出BM=CM=10，再根据E、F分别是线段BM、CM的中点，即可得出EM=FM=5，再根据N是边BC的中点，得出EM=FN，EN=FM，从而得出四边形ENFM的周长．
详解：∵M、N分别是边AD、BC的中点，AB=8，AD=12，
∴AM=DM=6，
∵四边形ABCD为矩形，
∴∠A=∠D=90°，
∴BM=CM=10，
∵E、F分别是线段BM、CM的中点，
∴EM=FM=5，
∴EN，FN都是△BCM的中位线，
∴EN=FN=5，
∴四边形ENFM的周长为5+5+5+5=20．
练习册系列答案
一线名师提优试卷系列答案
相关题目
