题目内容
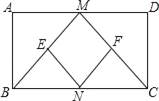
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上,三角形AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②AG=2GC,③BE+DF=EF,④S△CEF=2S△ABE正确的有_____(只填序号).
【答案】①④.
【解析】分析:先通过证明Rt△ABE≌Rt△ADF可对①进行判断;再证明AG垂直平分EF得到CG=![]() EF,即EF=2CG,则利用EF>AG可对②进行判断;由于∠EAG=30°,∠BAE=15°,则可判断BE≠EG,然后利用BE+DF=2BE,EF=2EG可对③进行判断;延长CB到F′使BF′=DF,作EH⊥AF′于H,如图,易得△ABF′≌△ABE,∠EAF′=30°,设CG=x,则EG=GF=x,AE=2x,所以EH=x,然后根据三角形面积公式可对④进行判断.
EF,即EF=2CG,则利用EF>AG可对②进行判断;由于∠EAG=30°,∠BAE=15°,则可判断BE≠EG,然后利用BE+DF=2BE,EF=2EG可对③进行判断;延长CB到F′使BF′=DF,作EH⊥AF′于H,如图,易得△ABF′≌△ABE,∠EAF′=30°,设CG=x,则EG=GF=x,AE=2x,所以EH=x,然后根据三角形面积公式可对④进行判断.
详解:∵△AEF为等边三角形,
∴AE=AF,
∵四边形ABCD为正方形,
∴AB=AD,∠B=∠D=∠BAD=90°,
在Rt△ABE和Rt△ADF中
![]()
∴Rt△ABE≌Rt△ADF,
∴BE=DF,所以①正确;
∠BAE=∠DAF,
∵AC平分∠BAD,
∴∠BAG=∠FAG,
∴AG垂直平分EF,
∴CG=![]() EF,即EF=2CG,
EF,即EF=2CG,
而EF>AG,
∴AG<2CG,所以②错误;
∵∠EAG=30°,∠BAE=15°,
∴BE≠EG,
∴BE+DF=2BE,EF=2EG,
∴BE+DF≠EF,所以③错误;
延长CB到F′使BF′=DF,作EH⊥AF′于H,如图,
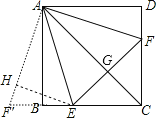
易得△ABF′≌△ABE,
∴∠EAF′=30°,
设CG=x,则EG=GF=x,AE=2x,
∴EH=x,
∴S△AF′E=![]() 2xx=x2,S△CEF=
2xx=x2,S△CEF=![]() x2x=x2,
x2x=x2,
∴S△CEF=2S△ABE,所以④正确.
故答案为①④.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目