Question

【题目】如图在直角坐标系中△ABC的顶点A、B、C三点坐标为A(7，1)，B(8，2)，C(9，0)．

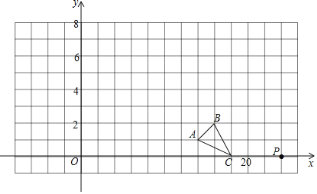
（1）请在图中画出△ABC的一个以点P(12，0)为位似中心，相似比为3的位似图形△A'B'C'（要求与△ABC在P点同一侧）；

（2）直接写出A'点的坐标；

（3）直接写出△A'B'C'的周长．

Answer 1

【答案】（1）见解析；（2）A′(﹣3，3)，B′(0，6)，C′(0，3)；（3）．

【解析】

（1）延长PB到B′，使PB′＝3PB，延长PA到B′，使PA′＝3PA，延长PC到C′，使PC′＝3PC；顺次连接A′、B′、C′，即可得到△A'B'C′；

（2）利用（1）所画图形写出A′点的坐标即可；

（3）利用勾股定理计算出A′B′、B′C′、A′C′，然后求它们的和即可．

（1）如图，△A′B′C′，为所作；

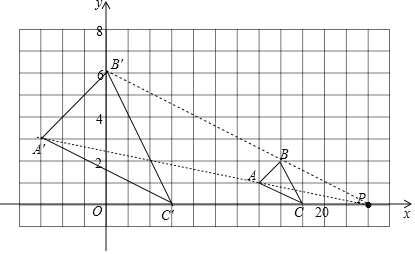
（2）A′、B′、C′三点的坐标分别是：A′（﹣3，3），B′（0，6），C′（0，3）；

（3）A′B′＝＝3，A′C′＝＝3，B′C′＝＝3，

所以△A′B′C′的周长＝3+3+3＝．