Question

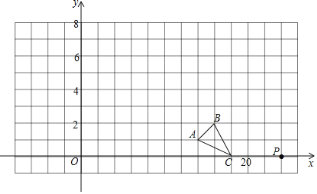
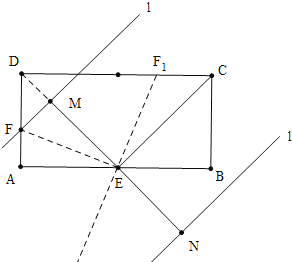
【题目】如图矩形，AB＝2BC＝4，E是AB二等分点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，沿直线EF折叠矩形ABCD，使点A落在直线l上，则DF＝_____．

Answer 1

【答案】2或4﹣2

【解析】

分两种情况求解：直线l在直线CE上方时，连接DE证得△ADE、△ECB是等腰直角三角形，由此证得点A、点M关于直线EF对称，利用已知数据求得DF；直线l在直线EC下方时，利用对顶角相等得到∠DEF1＝∠BEF1＝∠DF1E，求出DF1＝DE＝2.

如图，当直线l在直线CE上方时，连接DE交直线l于M，

∵AB＝2BC＝4，E是AB二等分点，

∴BC＝2，BE＝2＝AE

∵四边形ABCD是矩形，

∴∠A＝∠B＝90°，AD＝BC，

∵AB＝4，AD＝BC＝2，

∴AD＝AE＝EB＝BC＝2，

∴△ADE、△ECB是等腰直角三角形，

∴∠AED＝∠BEC＝45°，

∴∠DEC＝90°，

∵l∥EC，

∴ED⊥l，

∴EM＝2＝AE，

∴点A、点M关于直线EF对称，

∵∠MDF＝∠MFD＝45°，

∴DM＝MF＝DE﹣EM＝2﹣2，

∴DF＝DM＝4﹣2，

当直线l在直线EC下方时，

∵∠DEF1＝∠BEF1＝∠DF1E，

∴DF1＝DE＝2，

综上所述DF的长为2或4﹣2．

故答案为2或4﹣2．