题目内容
【题目】如图,在△ABC中,∠ACB=90°,AB=10,AC=6.动点P从点A出发,沿折线AC﹣CB运动,在边AC上以每秒3个单位长度的速度运动,在边BC上以每秒4个单位长度的速度运动,到点B停止,当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB于点Q;以Q为直角顶点向PQ右侧作Rt△PQD,且QD=![]() PQ.设△PQD与△ABC重叠部分图形的面积为S,点P运动的时间为t(s).
PQ.设△PQD与△ABC重叠部分图形的面积为S,点P运动的时间为t(s).
(1)当点P在边AC上时,求PQ的长(含t的代数式表示);
(2)点D落在边BC上时,求t的值;
(3)求S与t之间的函数关系式;
(4)设PD的中点为E,作直线CE.当直线CE将△PQD的面积分成1:5两部分时,直接写出t的值.

【答案】(1)PQ=4t;(2)t=![]() ;(3)S=
;(3)S=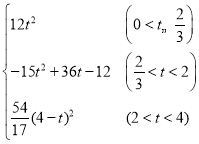 ;(4)
;(4)![]() 或
或![]() .
.
【解析】
(1)由PQ∥BC,推出△APQ∽△ACB,可得 ![]() ,由此构建关系式即可解决问题.
,由此构建关系式即可解决问题.
(2)当点D落在BC上时,四边形PCDQ是矩形,根据PC=DQ,构建方程解决问题即可.
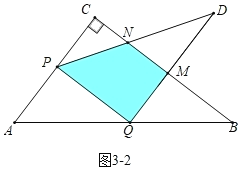
(3)分三种情形:①如图3﹣1中,当0<t≤![]() 时,重叠部分是△PQD.②如图3﹣2中,当
时,重叠部分是△PQD.②如图3﹣2中,当![]() <t<2时,重叠部分是四边形PQMN.③如图3﹣3中,当2<t<4时,重叠部分是△PQN,分别求解即可.
<t<2时,重叠部分是四边形PQMN.③如图3﹣3中,当2<t<4时,重叠部分是△PQN,分别求解即可.
(4)分两种情形:①如图4﹣1中,设直线CE交DQ于N,连接OE.当QN=2DN时,直线CE将△PQD的面积分成1:5两部分.②如图4﹣2中,如图4﹣2中,设直线CE交PQ于N,连接OE,延长QD交CE于M.当QN=2PN时,直线CE将△PQD的面积分成1:5两部分,分别求解即可.
解:(1)如图1中,当点P在AC上时,
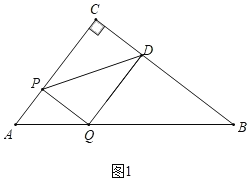
在Rt△ABC中,∵∠C=90°,AB=10,AC=6,
∴BC=![]() =8.
=8.
∵PQ∥BC,∴△APQ∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴PQ=4t.
(2)当点D落在BC上时,四边形PCDQ是矩形,∴PC=DQ.
∵PQ=4t,DQ=![]() PQ,
PQ,
∴DQ=6t,
∴6﹣3t=6t,
解得:t=![]() .
.
(3)①如图3﹣1中,当0<t≤![]() 时,重叠部分是△PQD.
时,重叠部分是△PQD.
S=![]() PQDQ=
PQDQ=×4t×6t=12t2.
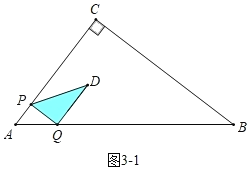
②如图3﹣2中,当![]() <t<2时,重叠部分是四边形PQMN,
<t<2时,重叠部分是四边形PQMN,
S=S△PQD﹣S△DMN=12t2﹣![]() ×(9t﹣6)×
×(9t﹣6)×![]() (9t﹣6)=﹣15t2+36t﹣12.
(9t﹣6)=﹣15t2+36t﹣12.
③如图3﹣3中,当2<t<4时,重叠部分是△PQN,

由题意PC=4(t﹣2),PB=BC﹣PC=16﹣4t=4(4﹣t),
∴PQ=3(4﹣t),DQ=![]() (4﹣t).
(4﹣t).
∵PB∥DQ,∴PN:DN=PB:DQ=8:9,
∴S=![]() S△PQD=
S△PQD=![]()
![]() 3(4﹣t)
3(4﹣t)![]() (4﹣t)=
(4﹣t)=![]() (4﹣t)2.
(4﹣t)2.
综上所述: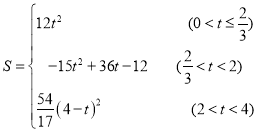 .
.
(4)①如图4﹣1中,设直线CE交DQ于N,连接OE.

当QN=2DN时,直线CE将△PQD的面积分成1:5两部分.
∵PE=DE,PC∥DN,
∴![]() ,∴PC=DN,
,∴PC=DN,
∴QN=2PC,DQ=3PC,
∴6t=3(6﹣3t),
∴t=![]() .
.
②如图4﹣2中,如图4﹣2中,设直线CE交PQ于N,连接OE,延长QD交CE于M.
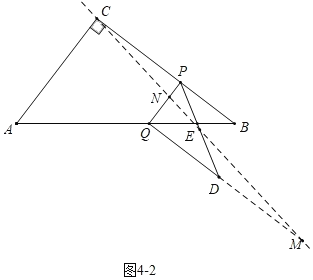
当QN=2PN时,直线CE将△PQD的面积分成1:5两部分.
∵PC∥QM,PE=ED,
∴![]() ,
,![]() ,
,
∴PC=DM=4(t﹣2),QM=2PC,
∴![]() (4﹣t)+4(t﹣2)=2×4(t﹣2),
(4﹣t)+4(t﹣2)=2×4(t﹣2),
解得:t=![]() ,
,
综上所述:满足条件的t的值为![]() 或
或![]() .
.

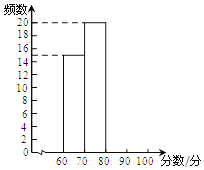
【题目】某学校组织七年级学生进行“垃圾分类”知识测试,现随机抽取部分学生的成绩进行统计,并绘制如下频数分布表以及频数分布直方图.
分数档 | 分数段/分 | 频数 | 频率 |
A | 90<x≤100 | a | 0.12 |
B | 80<x≤90 | b | 0.18 |
C | 70<x≤80 | 20 | c |
D | 60<x≤70 | 15 | d |
请根据以上信息,解答下列问题:
(1)已知A,B档的学生人数之和等于D档学生人数,求被抽取的学生人数,并把频数分布直方图补充完整.
(2)该校七年级共有200名学生参加测试,请估计七年级成绩在C档的学生人数.
(3)你能确定被抽取的这些学生的成绩的众数在哪一档吗?请说明理由.