题目内容
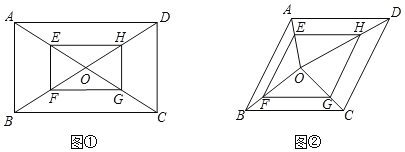
【题目】如图，正方形
的边长为
，
，
，
，
分别是
，
，
，
上的动点，且
．
（1）求证：四边形
是正方形；
（2）求四边形面积的最小值．
【答案】（1）详见解析；（2）四边形
面积的最小值为32．
【解析】
(1)由正方形的性质得出.∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA，证出AH=BE=CF=DG，由SAS证明△AEH≌△BFE≌△CGF≌△DHG，得出EH=FE=GF=GH,
∠AEH=∠BFE，证出四边形EFGH是菱形，再证出∠HEF=90°，即可得出结论;
(2)设四边形EFGH面积为S，AE=xcm,则BE=(8-x)cm,由勾股定理得出S=x2+(8-x)2=2(x-4)2+32,S是x的二次函数，容易得出四边形EFGH面积的最小值.
证明：（1）∵四边形
是正方形，
∴
，
．
∵
，∴
．
∴
，
∴
，
，
，
∴四边形是菱形，
∵
，
，
，
∴四边形是正方形．
（2）设
，
则
，
S四边形EFGH
，
∴当
时，四边形面积的最小值为32．
练习册系列答案
相关题目
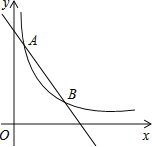
【题目】小明根据学习函数的经验，对函数y＝
+1的图象与性质进行了探究．下面是小明的探究过程，请补充完整：
（1）函数y＝+1的自变量x的取值范围是 ；
（2）下表列出了y与x的几组对应值，请写出m，n的值：m＝ ，n＝ ；
x | … | ﹣ | ﹣1 | ﹣ | 0 |
|
| 2 |
| 3 |
| … |
y | … |
| m |
| 0 | ﹣1 | n | 2 |
|
|
| … |
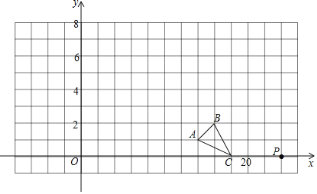
（3）在如图所示的平面直角坐标系中，描全上表中以各对对应值为坐标的点，并画出该函数的图象．
（4）结合函数的图象，解决问题：
①写出该函数的一条性质：
②当函数值+1＞
时，x的取值范围是：
③方程+1＝x的解为：
