题目内容
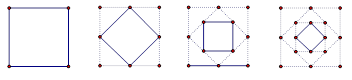
P、Q、R、S四个小球分别从正方形ABCD的四个定点A、B、C、D点出发,以同样的速度分别沿AB、BC、CD、DA的方向滚动,其终点分别是B、C、D、A。

(1)不管滚动多长时间,求证:四边形PQRS为正方形;
(2)连结对角线AC、BD、PR、SQ,你发现四条对角线有何关系?
(3)根据此图,若有四个全等的直角三角形,你能否拼成一个正方形?若这个三角形直角边为a、b,斜边问c,你能否根据面积推导出勾股定理?

(1)不管滚动多长时间,求证:四边形PQRS为正方形;
(2)连结对角线AC、BD、PR、SQ,你发现四条对角线有何关系?
(3)根据此图,若有四个全等的直角三角形,你能否拼成一个正方形?若这个三角形直角边为a、b,斜边问c,你能否根据面积推导出勾股定理?
(1)见解析(2)四条对角线相交于一点,且互相平分(3)能拼成一个正方形,见解析
(1)四个动点,P、Q、E、F分别从正方形ABCD的顶点A、B、C、D同时出发,沿着AB、BC、CD、DA以同样速度向B、C、D、A移动可得AP=BQ=CF=DS,PB=QC=FD=SA.
可得△APS≌△BQP≌△CFQ≌△DFS,
得PQ=QF=FS=SP.
∠SPA=∠PQB.
又∠PQB+∠QPB=90°,
所以∠FPA+∠QPB=90°,∠FPQ=90°.
所以PQEF为正方形.(3分)
(2)四条对角线相交于一点,且互相平分.(1分)
(3)能拼成一个正方形.用面积的方法来证明
直角边分别是a,b.斜边是c,
整个大正方形的面积应该是(a+b)2
而一个一个进行分解计算,4个小三角形的面积是4× ab=2ab.
ab=2ab.
中间的正方形面积是c2
则(a+b)2=2ab+c2,分解开就可以得到a2+b2=c2.(4分)
(1)可先证明△APF≌△BQP≌△CEQ≌△DFE,得PQ=QE=EF=FP;再证∠FPQ=90°;
(2)用面积的方法来证明,拼出的大正方形的面积,既可以用正方形面积公式求得,也可以用中间四个小三角形和小正方形的面积和来表示,列出相等关系,即可求证.
可得△APS≌△BQP≌△CFQ≌△DFS,
得PQ=QF=FS=SP.
∠SPA=∠PQB.
又∠PQB+∠QPB=90°,
所以∠FPA+∠QPB=90°,∠FPQ=90°.
所以PQEF为正方形.(3分)
(2)四条对角线相交于一点,且互相平分.(1分)
(3)能拼成一个正方形.用面积的方法来证明
直角边分别是a,b.斜边是c,
整个大正方形的面积应该是(a+b)2
而一个一个进行分解计算,4个小三角形的面积是4×
 ab=2ab.
ab=2ab.中间的正方形面积是c2
则(a+b)2=2ab+c2,分解开就可以得到a2+b2=c2.(4分)
(1)可先证明△APF≌△BQP≌△CEQ≌△DFE,得PQ=QE=EF=FP;再证∠FPQ=90°;
(2)用面积的方法来证明,拼出的大正方形的面积,既可以用正方形面积公式求得,也可以用中间四个小三角形和小正方形的面积和来表示,列出相等关系,即可求证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.

 中,
中, 且
且 ,
, 、
、 分别是两底的中点,连结
分别是两底的中点,连结 ,若
,若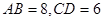 ,求
,求