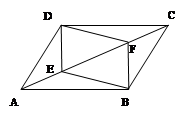题目内容
如图,在□ABCD中，AB=3，AD=4，∠ABC=60°，过BC的中点E作EF⊥AB，垂足为点F，与DC的延长线相交于点H，则△DEF的面积是 .
2
∵四边形ABCD是平行四边形，∴AD=BC=4，AB∥CD，AB=CD=3，
∵E为BC中点，∴BE=CE=2，∵∠B=60°，EF⊥AB，∴∠FEB=30°，
∴BF=1，由勾股定理得：EF=，∵AB∥CD，∴△BFE∽△CHE，
∴
=1，∴EF=EH=，CH=BF=1，
∵S△DHF=
DH•FH=×（1+3）×2=4，∴S△DEF=S△DHF=2．
∵E为BC中点，∴BE=CE=2，∵∠B=60°，EF⊥AB，∴∠FEB=30°，
∴BF=1，由勾股定理得：EF=
，∵AB∥CD，∴△BFE∽△CHE，∴
=1，∴EF=EH=，CH=BF=1，∵S△DHF=
DH•FH=×（1+3）×2=4，∴S△DEF=S△DHF=2．
练习册系列答案
阅读快车系列答案
相关题目
,点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.
的顶点
、
在数轴上，
，点
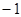，则点
