题目内容
如图，在正方形ABCD中，△APD是正三角形，则∠BPC= 
150°
∵四边形ABCD为正方形，
∴∠DAB=∠ABC=90°，
∵△APD是正三角形，
∴∠DAP=60°，
∴∠BAP=30°，
∵AP=AD=AB，
∴∠ABP=∠APB=（180°-∠BAP）÷2=150°÷2=75°，
∴∠PBC=∠PCB=∠ABC-∠ABP=90°-75°=15°，
∴∠BPC=180°-∠PBC-∠PCB=180°-15°-15°=150°
∴∠DAB=∠ABC=90°，
∵△APD是正三角形，
∴∠DAP=60°，
∴∠BAP=30°，
∵AP=AD=AB，
∴∠ABP=∠APB=（180°-∠BAP）÷2=150°÷2=75°，
∴∠PBC=∠PCB=∠ABC-∠ABP=90°-75°=15°，
∴∠BPC=180°-∠PBC-∠PCB=180°-15°-15°=150°
练习册系列答案
相关题目
的面积为12，
是等边三角形，点
在正方形
上有一点
， 使
的和最小，则这个最小值为（ ）
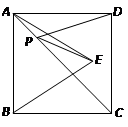
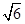
cm/s的速度，沿AC向C作匀速运动；与此同时，点Q也从A点出发，以1cm/s的速度，沿射线AB作匀速运动．当P运动到C点时，P、Q都停止运动．设点P运动的时间为ts．
