题目内容
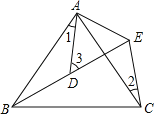
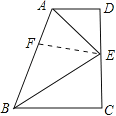
【题目】如图,在直角梯形ABCD中,AD∥BC,∠D=∠C=90°,点E在DC上,且AE,BE分别平分∠BAD和∠ABC.
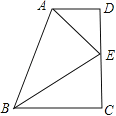
(1)求证:点E为CD中点;
(2)当AD=2,BC=3时,求AB的长.
【答案】(1)见试题解析(2)5.
【解析】
试题(1)过点E作EF⊥AB于F,利用已知条件可证明△ADE≌△AFE,由全等三角形的性质可得DE=FE,同理可证明EF=EC,所以DE=EF=CE,即点E为CD中点;
(2)由(1)可知AF=AD,BC=BF,所以AB=AF+BF=AD+BC=5,问题得解.
试题解析:(1)证明:过点E作EF⊥AB于F,∴∠AFE=90°,∴∠D=∠AFE=90°,∵AE平分∠BAD,
∴∠DAE=∠FAE,在△ADE和△AFE中,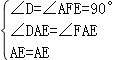 ,∴△ADE≌△AFE(AAS),
,∴△ADE≌△AFE(AAS),
∴DE=FE,同理可得:EF=EC,∴DE=EF=CE,即点E为CD中点;
(2)∵△ADE≌△AFE,∴AF=AD=2,BC=BF=3,∴AB=AF+BF=AD+BC=5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目