题目内容
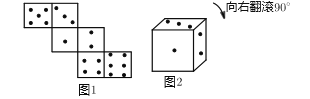
【题目】图①是正方体的平面展开图，六个面的点数分别为1点、2点、3点、4点、5点、6点，将点数朝外折叠成一枚正方体骰子，并放置于水平桌面上，如图②所示，若骰子初始位置为图②所示的状态，将骰子向右翻滚
，则完成1次翻转，此时骰子朝下一面的点数是2，那么按上述规则连线完成2次翻折后，骰子朝下一面的点数是3点；连续完成2019次翻折后，骰子朝下一面的点数是（ ）
A.2B.3C.4D.5
【答案】D
【解析】
根据正方体的表面展开图，可得各个面上的数字，由2019次翻转为第505组的第三次翻转，即可得到答案．
正方体的表面展开图，相对面之间一定相隔一个正方形，
“2点”与“5点”是相对面，“3点”与“4点”是相对面，“1点”与“6点”是相对面，
∵
，
∴完成2019次翻转为第505组的第三次翻转，
∴骰子朝下一面的点数是5．
故选D．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
