题目内容
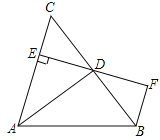
【题目】已知如图，D是△ABC的边AB上一点，DE∥BC，交边AC于点E，延长DE至点F，使EF＝DE，连接BF，交边AC于点G，连接CF.
(1)求证：
；
(2)如果CF2＝FG·FB，求证：CG·CE＝BC·DE.
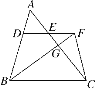
【答案】（1）见解析；（2）见解析.
【解析】分析: （1）首先证明△ADE∽△ABC，△EFG∽△CBG，根据相似三角形的对应边的比相等，以及DE=EF即可证得；
（2）首先证明△CFG∽△BFC，证得
＝
，∠FCE=∠CBF，然后根据平行线的性质证明∠FEG=∠CEF，即可证得△EFG∽△ECF，则
＝，即可证得＝
，则所证结论即可得到.
详解:
(1)∵DE∥BC，
∴△ADE∽△ABC，△EFG∽△CBG，
∴
＝
，
＝
.
又∵DE＝EF，
∴＝，
∴＝；
(2)∵CF2＝FG·FB，
∴
＝
.
又∠BFC＝∠CFG，
∴△BCF∽△CGF，
∴＝，∠FCE＝∠CBF.
又∵DF∥BC，
∴∠EFG＝∠CBF，
∴∠FCE＝∠EFG.
∵∠FEG＝∠CEF，
∴△EFG∽△ECF，
∴＝.
又∵EF＝DE，＝，
∴＝，即CG·CE＝BC·DE.
黄冈小状元同步计算天天练系列答案
【题目】我县木瓜村盛产优种红富士苹果，曾推选参加省农产品博览会，某人去该地水果批发市场采购苹果，他看中了A、B两家苹果．这两家苹果品质都一样，市场售价都为6元/千克，但批发进价不相同．两家苹果批发进价如下：
A家规定：批发数量不超过1000千克，可按市场售价的92%优惠；批发数量多于1000千克但不超过2000千克，可全部按市场售价的90%优惠；批发数超过2000千克则全部按市场售价的88%优惠．
B家的规定如下表：
数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上部分 |
批发进价(元) | 市场售价的95% | 市场售价的85% | 市场售价的75% | 市场售价的70% |
[表格说明： 
家苹果批发进价按分段计算，如：某人要批发苹果2100千克，则批发进价
]
根据上述信息，请解答下列问题：
（1）如果此人要批发1000千克苹果，则他在
家批发需要_______元，在家批发需要_______元；
（2）如果此人批发
千克苹果(1500<x<2000)，则他在家批发需要_______元，在家批发需要_______元（用含的代数式表示）；
（3）现在此人要批发3000千克苹果，你能帮助他选择在哪家批发更优惠吗?请说明理由．
