题目内容
【题目】【操作发现】
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
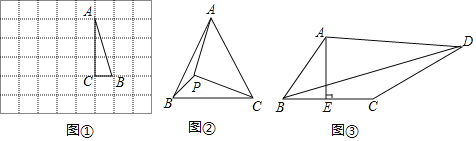
(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B= .
【问题解决】
如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
【灵活运用】
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示).
【答案】【操作发现】(1)作图见解析;(2)45°;【问题解决】7![]() ;【灵活运用】
;【灵活运用】![]() .
.
【解析】试题分析:【操作发现】(1)根据旋转角,旋转方向画出图形即可;(2)只要证明△ABB′是等腰直角三角形即可;【问题解决】如图②,将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,只要证明∠PP′C=90°,利用勾股定理即可解决问题;【灵活运用】如图③中,由AE⊥BC,BE=EC,推出AB=AC,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,只要证明∠GDC=90°,可得CG=![]() ,由此即可解决问题.
,由此即可解决问题.
试题解析:【操作发现】(1)如图所示,△AB′C′即为所求;
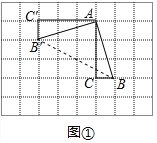
(2)连接BB′,将△ABC绕点A按顺时针方向旋转90°,
∴AB=AB′,∠B′AB=90°,
∴∠AB′B=45°,
故答案为:45°;
【问题解决】如图②,

∵将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,
∴△APP′是等边三角形,∠AP′C=∠APB=360°﹣90°﹣120°=150°,
∴PP′=AP,∠AP′P=∠APP′=60°,
∴∠PP′C=90°,∠P′PC=30°,
∴PP′=![]() PC,即AP=
PC,即AP=![]() PC,
PC,
∵∠APC=90°,
∴AP2+PC2=AC2,即(![]() PC)2+PC2=72,
PC)2+PC2=72,
∴PC=2![]() ,
,
∴AP=![]() ,
,
∴S△APC=![]() APPC=7
APPC=7![]() ;
;
【灵活运用】如图③中,∵AE⊥BC,BE=EC,
∴AB=AC,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,

∵∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴△ABC∽△ADG,
∵AD=kAB,
∴DG=kBC=4k,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADG+∠ADC=90°,
∴∠GDC=90°,
∴CG=![]() =
=![]() .
.
∴BD=CG=![]() .
.

【题目】近年来,我国很多地区持续出现雾霾天气.某社区为了调查本社区居民对雾霾天气主要成因的认识情况,随机对该社区部分居民进行了问卷调查,要求居民从五个主要成因中只选择其中的一项,被调查居民都按要求填写了问卷.社区对调查结果进行了整理,绘制了如下不完整的统计图表.被调查居民选择各选项人数统计表
雾霾天气的主要成因 | 频数(人数) |
A大气气压低,空气不流动 | m |
B地面灰尘大,空气湿度低 | 40 |
C汽车尾气排放 | n |
D工厂造成的污染 | 120 |
E其他 | 60 |
请根据图表中提供的信息解答下列问题:
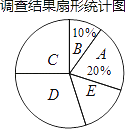
(1)填空:m=________,n=________,扇形统计图中C选项所占的百分比为________.
(2)若该社区居民约有6 000人,请估计其中会选择D选项的居民人数.
(3)对于“雾霾”这个环境问题,请你用简短的语言发出倡议.