题目内容
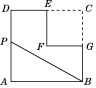
【题目】(本题满分10分)如图,将□ABCD沿过点A的直线![]() 折叠,使点D落到AB边上的点
折叠,使点D落到AB边上的点![]() 处,折痕
处,折痕![]() 交CD边于点E,连接BE
交CD边于点E,连接BE
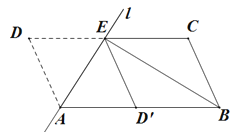
(1)求证:四边形![]() 是平行四边形
是平行四边形
(2)若BE平分∠ABC,求证:![]()
【答案】见解析
【解析】试题(1)根据翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,然后根据平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形;
(2)根据平行线的性质利用勾股定理得出答案.
试题解析:(1)∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,∴∠DEA=∠EAD′,∴∠DAE=∠EAD′=∠DEA=∠D′EA,∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,∴DE=AD′,
∵四边形ABCD是平行四边形,∴AB![]() DC,∴CE
DC,∴CE![]() D′B,∴四边形BCED′是平行四边形;
D′B,∴四边形BCED′是平行四边形;
(2)∵BE平分∠ABC,∴∠CBE=∠EBA,
∵AD∥BC,∴∠DAB+∠CBA=180°,
∵∠DAE=∠BAE,∴∠EAB+∠EBA=90°,∴∠AEB=90°,∴AB2=AE2+BE2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目