题目内容
【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.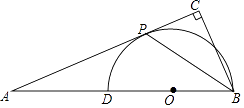
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
【答案】
(1)证明:连接OP,
∵AC是⊙O的切线,
∴OP⊥AC,BC⊥AC,
∴OP∥BC,
∴∠OPB=∠PBC,
∵OP=OB,
∴∠OPB=∠OBP,
∴∠PBC=∠OBP,
∴BP平分∠ABC
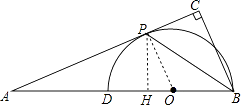
(2)作PH⊥AB于H.
∵PB平分∠ABC,PC⊥BC,PH⊥AB,
∴PC=PH=1,
在Rt△APH中,AH= ![]() =2
=2 ![]() ,
,
∵∠A=∠A,∠AHP=∠C=90°,
∴△APH∽△ABC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AB=3 ![]() ,
,
∴BH=AB﹣AH= ![]() ,
,
在Rt△PBC和Rt△PBH中,
![]() ,
,
∴Rt△PBC≌Rt△PBH,
∴BC=BH= ![]() .
.
【解析】(1) 根据切线的性质易证OP∥BC,由平行线的性质定理得∠OPB=∠PBC,由等边对等角得∠OPB=∠OBP,进而∠PBC=∠OBP,即BP平分∠ABC;(2) 作PH⊥AB于H. 由角平分线的性质定理得PC=PH=1,在Rt△APH中由勾股定理得AH得长 度,进而判断出△APH∽△ABC,再由相似三角形的对应边成比例得出AB的长,进而得出BH的长,再证出Rt△PBC≌Rt△PBH,由全等三角形对应边成比例就可以得出结论。
【考点精析】掌握角平分线的性质定理和勾股定理的概念是解答本题的根本,需要知道定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目