题目内容
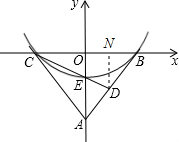
如图，在平面直角坐标系xOy中，AO=8，AB=AC，sin∠ABC=
．CD与y轴交于点E，且S△COE=S△ADE．已知经过B，C，E三点的图象是一条抛物线，求这条抛物线对应的二次函数的解析式．
| 4 |
| 5 |
过点D作DN⊥BC，
∵AB=AC，AO⊥BC，
∴BO=CO，
∵sin∠ABC=
，AO=8，
∴sin∠ABC=
=
=
，
∴AB=10，
BO=
=6，
∴B点坐标为：（6，0），C点坐标为：（-6，0），
∵S△COE=S△ADE，
∴S△CDB=S△ABO，
∴DN×BC=AO×BO，
∴DN=
=
=4，
∵ND∥AO，
∴
=
=
，
∴NO=NB=3，
∴
=
，
∴
=
，
解得：EO=
，
∴E点坐标为：（0，-
），
∵经过B，C，E三点的图象对称轴为y轴，
∴经过B，C，E三点的解析式为：y=ax2+c，
将E点坐标为：（0，-
），B点坐标为：（6，0）代入解析式得：
，
解得：
，
∴这条抛物线对应的二次函数的解析式为：y=
x2-
．
∵AB=AC，AO⊥BC，
∴BO=CO，
∵sin∠ABC=
| 4 |
| 5 |
∴sin∠ABC=
| AO |
| AB |
| 8 |
| AB |
| 4 |
| 5 |
∴AB=10，
BO=
| 102-82 |
∴B点坐标为：（6，0），C点坐标为：（-6，0），
∵S△COE=S△ADE，
∴S△CDB=S△ABO，
∴DN×BC=AO×BO，
∴DN=
| AO•BO |
| BC |
| 8×6 |
| 12 |
∵ND∥AO，
∴
| DN |
| AO |
| NB |
| BO |
| 1 |
| 2 |
∴NO=NB=3，
∴
| EO |
| ND |
| CO |
| CN |
∴
| EO |
| 4 |
| 6 |
| 9 |
解得：EO=
| 8 |
| 3 |
∴E点坐标为：（0，-
| 8 |
| 3 |
∵经过B，C，E三点的图象对称轴为y轴，
∴经过B，C，E三点的解析式为：y=ax2+c，
将E点坐标为：（0，-
| 8 |
| 3 |
|
解得：
|
∴这条抛物线对应的二次函数的解析式为：y=
| 2 |
| 27 |
| 8 |
| 3 |
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
）两点，设OA•OB=3（O为坐标系原点）．
