题目内容
是否存在这样的实数k,使得二次方程x2+(2k-1)x-(3k+2)=0有两个实数根,且两根都在2与4之间?如果有,试确定k的取值范围;如果没有,试述理由.
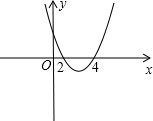
这样的k值不存在,理由如下:设y=f(x)=x2+(2k-1)x-(3k+2)并作出如图所示图象,则
,
整理得,
由②⑤可知,此不等式组无解,故k值不存在.
|
整理得,
|
由②⑤可知,此不等式组无解,故k值不存在.


练习册系列答案
相关题目

 其中曲线OAB为抛物线的一部分,点A为该抛物线的顶点,BC是线段.
其中曲线OAB为抛物线的一部分,点A为该抛物线的顶点,BC是线段.
 种不同于(3)的正确证明吗?我们将对你的出色表现另外奖励3分.
种不同于(3)的正确证明吗?我们将对你的出色表现另外奖励3分. 
