题目内容
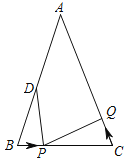
【题目】综合题:如图1，△ABC中，∠B=30°，AB=3，BC=4，则△ABC的面积等于
（1）【回顾】
如图1，△ABC中，∠B=30°，AB=3，BC=4，则△ABC的面积等于 ．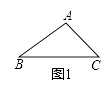 
（2）【探究】
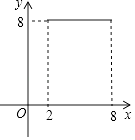
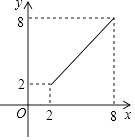
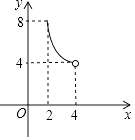
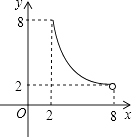
图2是同学们熟悉的一副三角尺，一个含有30°的角，较短的直角边长为a；另一个含有45°的角，直角边长为b，小明用两副这样的三角尺拼成一个平行四边形ABCD（如图3），用了两种不同的方法计算它的面积，从而推出sin75°= 
，小丽用两副这样的三角尺拼成了一个矩形EFGH（如图4），也推出sin75°= ，请你写出小明或小丽推出sin75°= 的具体说理过程．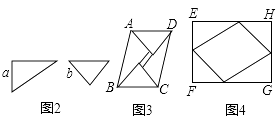
（3）【应用】
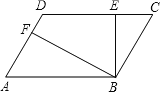
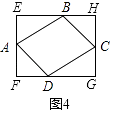
在四边形ABCD中，AD∥BC，∠D=75°，BC=6，CD=5，AD=10（如图5）
①点E在AD上，设t=BE+CE，求t2的最小值；
②点F在AB上，将△BCF沿CF翻折，点B落在AD上的点G处，点G是AD的中点吗？说明理由．
【答案】
（1）3
（2）如图3中，
由题意可知四边形EFGH是矩形，AB=CD=2a，AH=DH=BF=CF=b，EF=GH= 
a﹣b，EH=FG=b﹣a，BC= 
b，
∵S四边形ABCD=BCABsin75°=2S△ABE+2S△BFC+S矩形EFGH
∴ b2asin75°=2× 
×a× a+2× ×b2+（ a﹣b）（b﹣a），
∴2 absin75°= ab+ab，
∴sin75°= 
．
如图4中，
易知四边形ABCD是平行四边形，∠BAD=75°，
∴S四边形EFGH=2S△ABE+2S△ADF+S平行四边形ABCD，
∴（a+b）（ a+b）═2× ×a× a+2× ×b2+ b2asin75°，
∴sin75°= ．
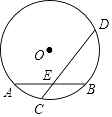
（3）①作C关于AD的对称点H，CH交AD于J，连接BH，EH．
在Rt△DCJ中，JC=CDsin75°= 
（ 
+ ），
∴CH=2CJ= 
（ ），
在Rt△BHC中，BH2=BC2+CH2=36+ 
（ + ）2=86+25 ，
∵EC=EH，
∴EB+EC=EB+EH，
在△EBH中，BE+EH≥BH，
∴BE+EC的最小值为BH，
∴t=BE+CE，t2的最小值为BH2，即为86+25 ．
②结论：点G不是AD的中点．
理由：作CJ⊥AD于J，DH⊥CG于H．
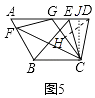
不妨设AG=GD=5，∵CD=5，
∴DC=DG，∵DH⊥CG，
∴GH=CH=3，
在Rt△CDH中，DH= 
= 
=4，
∵S△DGC= CGDH= DGCJ，
∴CJ= 
，
∴sin∠CDJ= 
= 
，
∵∠CDJ=75°，
∴与sin75°= 矛盾，
∴假设不成立，
∴点G不是AD的中点．
【解析】（1）由题意可知四边形EFGH是矩形，AB=CD=2a，AH=DH=BF=CF=b，EF=GH= a﹣b，EH=FG=b﹣a，BC= b，
回顾：如图1中，作AH⊥BC．
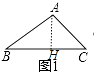
在Rt△ABH中，∵∠B=30°，AB=3，
∴AH=ABsin30°= 
，
∴S△ABC= BCAH= ×4× =3，
所以答案是3．
【考点精析】认真审题，首先需要了解锐角三角函数的定义(锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数)．
