题目内容
【题目】如图1，
，点
，
分别在
，
上，
射线
绕点顺时针旋转至
便立即逆时针回转，射线
绕点顺时针旋转至
便立即逆时针回转．射线转动的速度是每秒
度，射线转动的速度是每秒
度．
（1）直接写出
的大小为_______；
（2）射线、转动后对应的射线分别为
、
，射线交直线于点
，若射线比射线先转动
秒，设射线转动的时间为
秒，求为多少时，直线
直线？
（3）如图2，若射线、同时转动
秒，转动的两条射线交于点
，作
，点
在上，请探究
与
的数量关系．
【答案】（1）60°；（2）当
秒或
秒时
直线
；（3）
和
关系不会变化，
．
【解析】
(1)根据
得到
，再根据直线平行的性质即可得到答案；
(2)设灯转动t秒，直线直线，分情况讨论重合前平行、重合后平行即可得到答案；
(3)根据补角的性质表示出，再根据三角形内角和即可表示出，即可得到答案；
解：（1）∵
，
∴，
∴
（两直线平行，内错角相等）
故结果为：
；
（2）设灯转动t秒，直线直线，
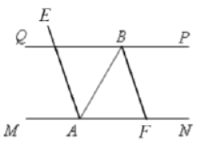
①当
时，如图，
，
，
，
，
，
，
解得；
②当
时，如图，
，
，
，
，
，
解得
，
综上所述，当秒或秒时直线；
（3）和关系不会变化，
理由：设射线AM转动时间为m秒，
作
，，
，
，
，
，
，
，
，
而
，
，
，
，
，
即，
和关系不变．
练习册系列答案
小学教材完全解读系列答案
相关题目
