题目内容
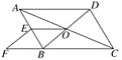
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.

【答案】(1)详见解析;(2)①详见解析;②:ME=BD,证明详见解析;③∠CNE的度数为7.5°、15°、82.5°、150°.
【解析】
(1)根据中垂线的判定定理“与一条线段两个端点距离相等的点,在这条线段的垂直平分线上”可得出结论.
(2)①由∠CAD=15°,BD=AD与直角等腰三角形的性质可知,∠DBA=∠DAB=30°,则可得∠BDE=30°+30°=60°,又根据SSS可证△ADC≌△BDC,则∠ACD=∠BCD=45°,可知∠CDE=∠ACD+∠CAD=45°+15°=60°,故DE平分∠BDC.
②连接MC,由DC=DM,∠CDE=60°,可知△MCD为等边三角形,∠ECM=∠CMD-∠CAD=45°则根据SAS可证△BDC≌△EMC,得出结论ME=BD.
③根据题意可知,分类:当EN=EC时;当EN=CN时;当CE=CN时三种情况求出∠CNE的度数.
(1)证明:∵CB=CA,DB=DA,
∴CD垂直平分线段AB,
∴CD⊥AB,
故答案为:CD⊥AB.
(2)①证明:∵AC=BC,
∴∠CBA=∠CAB,
又∵∠ACB=90°,
∴∠CBA=∠CAB=45°,
又∵在△ADC和△BDC中,
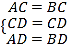 ,
,
∴△ADC≌△BDC(SSS),
∴∠CAD=∠CBD=15°,
∴∠DBA=∠DAB=30°,
∴∠BDE=30°+30°=60°,
∵∠ACB=90°,∠ACD=∠BCD,
∴∠ACD=∠BCD=45°,
∴∠CDE=∠ACD+∠CAD=45°+15°=60°,
∵∠CDE=∠BDE=60°,
∴DE平分∠BDC;
故答案为:DE平分∠BDC.
②结论:ME=BD,
理由:连接MC,

∵DC=DM,∠CDE=60°,
∴△MCD为等边三角形,
∴CM=CD,∠CMD=60°,
又∵EC=CA,∠CAD=15°,
∴∠ECM=∠CMD-∠CAD=45°,
在△BDC和△EMC中,
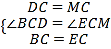 ,
,
∴△BDC≌△EMC(SAS),
∴ME=BD,
故答案为:ME=BD.
③当EN=EC时,∠ENC=7.5°或82.5°;
当EN=CN时,∠ENC=150°;
当CE=CN时,∠CNE=15°,
故答案为:∠CNE的度数为7.5°、15°、82.5°、150°.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案