题目内容
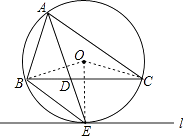
【题目】已知:如图,点A,B,C三点在⊙O上,AE平分∠BAC,交⊙O于点E,交BC于点D,过点E作直线l∥BC,连结BE. 
(1)求证:直线l是⊙O的切线;
(2)如果DE=a,AE=b,写出求BE的长的思路.
【答案】
(1)解:如图,连接OE、OB、OC,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴ ![]() ,
,
∴∠BOE=∠COE,
∵OB=OC,
∴OE⊥BC,
∵l∥BC,
∴OE⊥l,
∴直线l是⊙O的切线;
(2)∵∠BAE=∠CAE,∠CAE=∠CBE,
∴∠BAE=∠DBE,
又∵∠AEB=∠BED,
∴△ABE∽△BDE,
∴ ![]() =
= ![]() ,
,
∴BE2=AEDE=ab.
【解析】(1)作辅助线,连接半径,由角平分线得:∠BAE=∠CAE,圆周角相等,则弧相等,再由垂径定理证明OE⊥BC,所以OE⊥l,直线l与⊙O相切;(2)根据∠BAE=∠CAE、∠CAE=∠CBE结合公共角证△ABE∽△BDE可得 ![]() =
= ![]() ,从而得出答案.
,从而得出答案.

练习册系列答案
相关题目