��Ŀ����
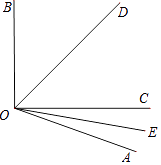
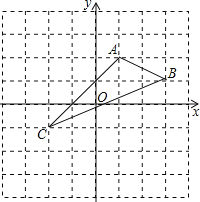
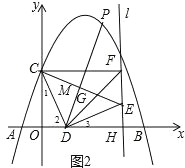
����Ŀ����ͼ��������y=ax2+bx+3��x����A����1��0����B��5��0������y���ڵ�C����D���߶�OB��һ���㣬����CD����CD�Ƶ�D˳ʱ����ת90��õ��߶�DE������E��ֱ��l��x�ᣬ����ΪH������C��CF��l��F������DF��CE���ڵ�G��
��1���������߽���ʽ��
��2�����߶�DF�ij���
��3����DG=![]() ʱ��
ʱ��
����tan��CGD��ֵ��
����̽����x���Ϸ����������ϣ��Ƿ���ڵ�P��ʹ��EDP=45�㣿�����ڣ���д����P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1�������߽���ʽΪ��y=��![]() x2+
x2+![]() x+3����2��DF=
x+3����2��DF=![]() =3
=3![]() ����3����tan��CGD=3��
����3����tan��CGD=3��
��P��������![]() ��
��![]() ����
����
��������
�����������1����A���B���������y=ax2+bx+3�еõ�����a��b�ķ����飬Ȼ��ⷽ�������a��b���ɵõ������߽���ʽ��
��2����ͼ1�������C�����꣬�ٸ�����ת�����ʵõ�CD=DE����CDE=90�㣬��֤����OCD�ա�HDE�õ�HD=OC=3������˵���ı���OCFHΪ���εõ�HF=OC=3��Ȼ�����ù��ɶ�������DF��
��3����������CDE����DFH���ǵ���ֱ�������εõ���DCE=45�㣬��DFH=45�㣬��������DFC=45�㣬���֤����DCG�ס�DFC���������Ƶ����ʵ�![]() =
=![]() ����DGC=��DCF�������������Ʊȿɼ����CD=
����DGC=��DCF�������������Ʊȿɼ����CD=![]() ��������DCF=��2�õ���CGD=��2��Ȼ����Rt��OCD�������2������ֵ���ɵõ�tan��CGD��ֵ��
��������DCF=��2�õ���CGD=��2��Ȼ����Rt��OCD�������2������ֵ���ɵõ�tan��CGD��ֵ��
�ڸ�����DCG�ס�DFC�õ�HD=OC=3��EH=OD=1����E��4��1����ȡCE���е�M����ͼ2�������߶ε��е����깫ʽ�õ�M��2��2�������ݵ���ֱ�������ε������ж�DP����CE���е�M�����������ô���ϵ�������ֱ��DP�Ľ���ʽΪy=2x��2��Ȼ��ⷽ����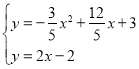 �ɵ�P�����꣮
�ɵ�P�����꣮
������������1����������y=ax2+bx+3��x����A����1��0����B��5��0����
��![]() �����
�����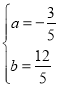 ���������߽���ʽΪ��y=��
���������߽���ʽΪ��y=��![]() x2+
x2+![]() x+3��
x+3��
��2����x=0ʱ��y=��![]() x2+
x2+![]() x+3=3����C��0��3������ͼ1��
x+3=3����C��0��3������ͼ1��
��CD�Ƶ�D˳ʱ����ת90��õ��߶�DE��
��CD=DE����CDE=90�㣬
�ߡ�2+��3=90�㣬
����1+��2=90�㣬
���1=��3��
����OCD����HDE��
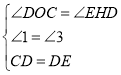 ��
��
���OCD�ա�HDE��
��HD=OC=3��
��CF��BF��
���ı���OCFHΪ���Σ�
��HF=OC=3��
��DF=![]() =3
=3![]() ��
��
��3�����ߡ�CDE����DFH���ǵ���ֱ�������Σ���ͼ1��
���DCE=45�㣬��DFH=45�㣬
���DFC=45�㣬
����CDG=��FDC��
���DCG�ס�DFC��
��![]() ����DGC=��DCF����
����DGC=��DCF����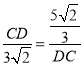 �����CD=
�����CD=![]() ��
��
��CF��OH��
���DCF=��2��
���CGD=��2��
��Rt��OCD��OD=![]() =
=![]() =1��
=1��
��tan��2=![]() =3��
=3��
��tan��CGD=3��
����OD=1��
��D��1��0����
�ߡ�OCD�ա�HDE��
��HD=OC=3��EH=OD=1��
��E��4��1����
ȡCE���е�M����ͼ2����M��2��2����
�ߡ�DCEΪ����ֱ�������Σ���EDP=45�㣬
��DP����CE���е�M��
��ֱ��DP�Ľ���ʽΪy=mx+n��
��D��1��0����M��2��2�������![]() �����
�����![]() ��
��
��ֱ��DP�Ľ���ʽΪy=2x��2��
�ⷽ����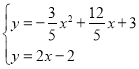 ��
�� ��
��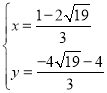 ����ȥ����
����ȥ����
����P��������![]() ��
��![]() ����
����


 ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�