题目内容
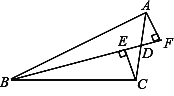
【题目】如图,已知BD为△ABC的中线,CE⊥BD于E,AF⊥BD于F.于是小白说:
“BE+BF=2BD”.你认为他的判断对吗?为什么?
【答案】对,理由详见解析.
【解析】试题分析:根据BD是中线得AD=CD,再根据CE⊥BD,AF⊥BD可以得到∠F=∠CED=90°,然后证明△AFD和△CED全等,再根据全等三角形对应边相等得DE=DE,再根据线段的和差关系即可证明.
试题解析:对.理由如下:
∵BD为△ABC的中线,
∴AD=CD,
∵CE⊥BD于E,AF⊥BD于F,
∴∠F=∠CED=90°,
在△AFD和△CED中,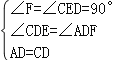 ,
,
∴△AFD≌△CED(AAS),
∴DE=DF,
∵BE+BF=(BD﹣DE)+(BD+DF),
∴BE+BF=2BD.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目