题目内容
【题目】如图,∠AOB=110°,OD平分∠BOC,OE平分∠AOC. 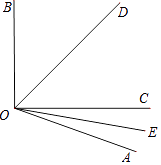
(1)求∠EOD的度数.
(2)若∠BOC=90°,求∠AOE的度数.
【答案】
(1)解:∵OD平分∠BOC,OE平分∠AOC,
∴∠COD= ![]() ∠BOC,∠COE=
∠BOC,∠COE= ![]() ∠AOC,
∠AOC,
∴∠EOD=∠COD+∠COE
= ![]() (∠BOC+∠AOC)
(∠BOC+∠AOC)
= ![]() ∠AOB
∠AOB
=55°
(2)解:由于∠AOC=∠AOB﹣∠BOC=110°﹣90°=20°,
∵OE平分∠AOC,
∴∠AOE= ![]() ∠AOC=10°
∠AOC=10°
【解析】(1)由OD平分∠BOC,OE平分∠AOC,可知∴∠EOD=∠COD+∠COE= ![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)= ![]() ∠AOB=55°;
∠AOB=55°;
【考点精析】利用角的平分线和角的运算对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.

练习册系列答案
相关题目
【题目】某公司为了评价甲、乙两位营销员去年的营销业绩,统计了这两人去年12个月的营销业绩(所推销商品的件数)分别如下图所示:
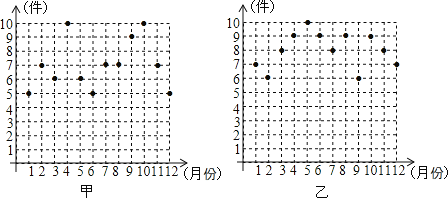
(1)利用图中信息,完成下表:
平均数 | 中位数 | 众数 | 方差 | |
甲 | 7 | |||
乙 | 1.5 |
(2)假若你是公司主管,请你根据(1)中图表信息,应用所学的统计知识,对两人的营销业绩作出评价.
