题目内容
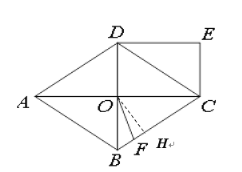
【题目】如图，菱形ABCD中，对角线AC、BD交于O点，DE∥AC，CE∥BD．
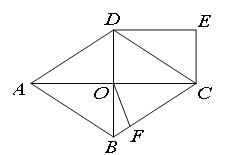
（1）求证：四边形OCED为矩形；
（2）在BC上截取CF＝CO，连接OF，若AC＝16，BD＝12，求四边形OFCD的面积．
【答案】（1）证明见解析；（2）
．
【解析】
（1）由DE∥AC，CE∥BD可得四边形OCED为平行四边形，又AC⊥BD从而得四边形OCED为矩形；
（2）过点O作OH⊥BC，垂足为H，由已知可得三角形OBC、OCD的面积，BC的长，由面积法可得OH的长，从而可得三角形OCF的面积，三角形OCD与三角形OCF的和即为所求．
（1）∵DE∥AC，CE∥BD，∴四边形OCED为平行四边形．又∵四边形ABCD是菱形，∴AC⊥BD．∴∠DOC=90°．∴四边形OCED为矩形．
（2）∵菱形ABCD，∴AC与BD互相垂直平分于点O，∴OD＝OB＝
BD＝6，OA＝OC＝AC＝8，∴CF=CO=8，S△BOC=S△DOC＝
＝24，在Rt△OBC中，BC＝
＝10，．作OH⊥BC于点H，则有BC·OH=24，∴OH=
，∴S△COF=CF·OH=
．∴S四边形OFCD＝S△DOC＋S△OCF＝.
练习册系列答案
相关题目
