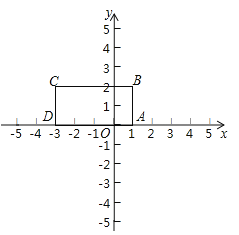Question

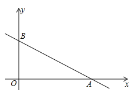
【题目】如图，在平面直角坐标系中，直线与x轴、轴分别交于点,，将点绕坐标原点顺时针旋转得点，解答下列问题:

（1）求出点的坐标，并判断点是否在直线l上；

（2）若点在x轴上，坐标平面内是否存在点，使得以、、、为顶点的四边形是菱形？若存在，请直接写出点坐标；若不存在，请说明理由．

Answer 1

【答案】（1），点在直线l上，见解析；（2）存在，点坐标为：，或，或或.

【解析】

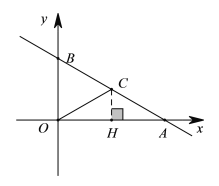
（1）依题意作出点，过C点作CH⊥OA，旋转性质可得，由30°直角三角形性质可求出HC=，OH=3，即可得出C点坐标，将C点坐标代入解析式验证，符合解析式即可判定C在直线l上.

即可求解；

（2）分是菱形的一条边、是菱形的一条对角线两种情况，分别根据点平移的规律求解即可．

解：（1）设将点绕坐标原点顺时针旋转得点，

直线，令，则，令，则，

则点、的坐标分别为、，，

则，，

∵，OC=OB=，

∴，

过C点作CH⊥OA，

∴HC=，OH=3

点C的坐标为；

∵当x=3时，=.

∴点的坐标在直线l上.

（2）存在，理由：

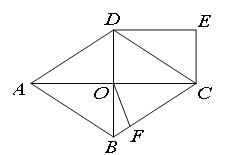
点、的坐标分别为、，则，以、、、为顶点的四边形是菱形如图所示，

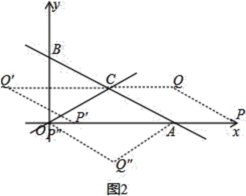
①当是菱形的一条边时，当点在x轴上方，

当菱形为时，则，则点，；

当菱形为时，点，；

当点在x轴下方，

同理可得：点；

②当是菱形的对角线时，

设点，点，

则的中点即为的中点，且（即，

，，，

解得：，，，

故点；

综上，点坐标为：，或，或或．