题目内容
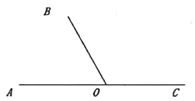
【题目】如图,在平面内,点![]() 是直线
是直线![]() 上一点,
上一点,![]() ,射线
,射线![]() 不动,射线
不动,射线![]() ,
,![]() 同时开始绕点
同时开始绕点![]() 顺时针转动,射线
顺时针转动,射线![]() 首次回到起始位置时两线同时停止转动,射线
首次回到起始位置时两线同时停止转动,射线![]() ,
,![]() 的转动速度分别为每秒
的转动速度分别为每秒![]() 和每秒
和每秒![]() .若转动
.若转动![]() 秒时,射线
秒时,射线![]() ,
,![]() ,
,![]() 中的一条是另外两条组成角的角平分线,则
中的一条是另外两条组成角的角平分线,则![]() ______秒.
______秒.
【答案】4或5
【解析】
根据已知条件可知,在第t秒时,射线OA转过的角度为40°t,射线OB转过的角度为20°t,然后按照OA、OB、OC三条射线构成相等的角分三种情况讨论:①当OA平分∠BOC;②当OC平分∠AOB;③当OB平分∠AOC,分别列方程即可求出t的值.
解:根据题意,在第t秒时,射线OA转过的角度为40°t,射线OB转过的角度为20°t,
①当OA,OB转到OA′,OB′的位置时,如图①所示,∠A′OC=∠A′OB′,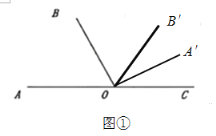
∵∠A′OC=180°-40°t,∠A′OB′=∠AOA′-∠AOB-∠BOB′=40°t-60°-20°t=20°t-60°,
∴180°-40°t =20°t-60°,
即t=4;
②当OA,OB转到OA′,OB′的位置时,如图②所示,∠A′OC=∠B′OC,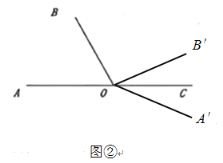
∵∠A′OC=40°t-180°,∠B′OC=180°-∠AOB-∠BOB′=180°-60°-20°t=120°-20°t,
∴40°t-180°=120°-20°t,
即t=5;
③当OA,OB转到OA′,OB′的位置时,如图③,∠B′OC=∠A′OB′,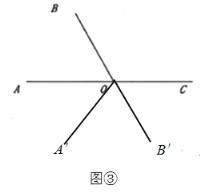
∵∠B′OC=20°t-120°,∠A′OB′=![]() ∠A′OC=
∠A′OC=![]() (180°-∠AOA′)=
(180°-∠AOA′)=![]() [180°-(360°-40°t)]=20°t-90°,
[180°-(360°-40°t)]=20°t-90°,
∴20°t-120°=20°t-90°,此时方程不成立.
综上所述:t的值为4或5.
故答案:4或5.

练习册系列答案
相关题目