题目内容
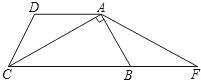
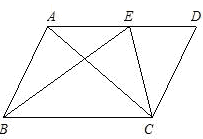
如图,在梯形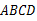 中,
中,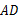 ∥
∥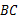 ,
,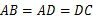 ,
,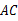 ⊥
⊥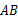 ,延长
,延长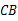 至点
至点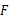 ,使
,使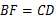 .
.
(1)求∠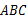 的度数.
的度数.
(2)试说明:△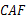 为等腰三角形.
为等腰三角形.
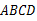 中,
中,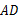 ∥
∥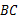 ,
,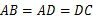 ,
,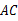 ⊥
⊥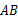 ,延长
,延长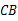 至点
至点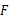 ,使
,使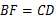 .
.
(1)求∠
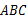 的度数.
的度数.(2)试说明:△
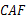 为等腰三角形.
为等腰三角形.(1)60° (2)见解析
分析:(1)在三角形中,根据等边对等角,再利用角的等量关系可知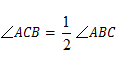 ,再由直角三角形中,两锐角互余即可求解.
,再由直角三角形中,两锐角互余即可求解.
(2)有两条边相等的三角形是等腰三角形,故连接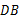 ,根据等腰梯形的性质及线段间的关系及平行的性质,可得
,根据等腰梯形的性质及线段间的关系及平行的性质,可得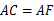 .
.
解:(1)∵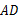 ∥
∥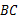 ,∴
,∴ 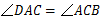 .
.
∵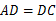 ,∴
,∴ 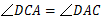 .
.
∴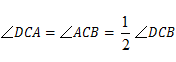 .
.
∵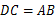 ,∴ 梯形
,∴ 梯形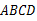 为等腰梯形,
为等腰梯形,
∴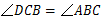 .∴
.∴ 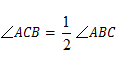 .
.
在△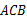 中,∵
中,∵  ,∴
,∴  .
.
∴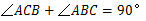 .∴
.∴ 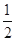
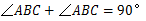 .∴
.∴ 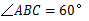 .
.
(2)如图,连接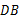 ,由等腰梯形
,由等腰梯形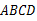 可得
可得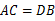 .
.

在四边形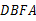 中,∵
中,∵ 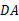 ∥
∥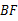 ,
,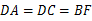 ,
,
∴ 四边形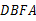 是平行四边形.∴
是平行四边形.∴ 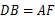 ,∴
,∴ 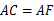 ,
,
即△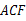 为等腰三角形.
为等腰三角形.
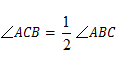 ,再由直角三角形中,两锐角互余即可求解.
,再由直角三角形中,两锐角互余即可求解.(2)有两条边相等的三角形是等腰三角形,故连接
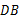 ,根据等腰梯形的性质及线段间的关系及平行的性质,可得
,根据等腰梯形的性质及线段间的关系及平行的性质,可得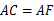 .
.解:(1)∵
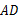 ∥
∥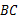 ,∴
,∴ 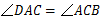 .
.∵
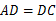 ,∴
,∴ 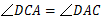 .
.∴
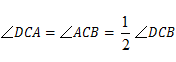 .
.∵
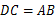 ,∴ 梯形
,∴ 梯形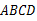 为等腰梯形,
为等腰梯形,∴
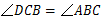 .∴
.∴ 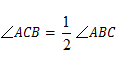 .
.在△
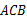 中,∵
中,∵  ,∴
,∴  .
.∴
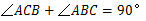 .∴
.∴ 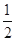
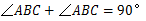 .∴
.∴ 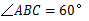 .
.(2)如图,连接
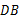 ,由等腰梯形
,由等腰梯形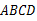 可得
可得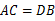 .
.
在四边形
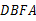 中,∵
中,∵ 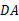 ∥
∥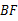 ,
,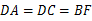 ,
,∴ 四边形
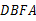 是平行四边形.∴
是平行四边形.∴ 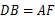 ,∴
,∴ 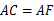 ,
,即△
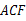 为等腰三角形.
为等腰三角形.
练习册系列答案
相关题目
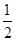 ∠BAD.
∠BAD.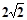 .求BC的长.
.求BC的长.
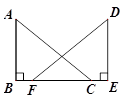
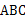 中,
中,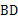 是角平分线,∠
是角平分线,∠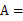 ∠
∠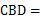 36°,则图中有等腰三角形( )
36°,则图中有等腰三角形( )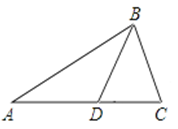
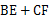 的大小关系是( )
的大小关系是( )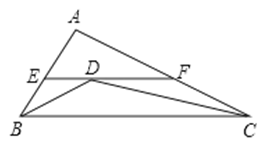
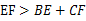 B.
B.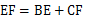
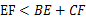 D.不能确定
D.不能确定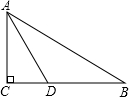
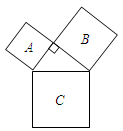
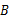 的面积为144,正方形
的面积为144,正方形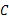 的面积为169时,那么正方形
的面积为169时,那么正方形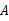 的面积为( )
的面积为( )