题目内容
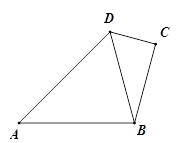
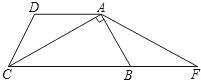
如图,在四边形ABCD中,∠A=45°,∠C=90°,∠ABD=75°,∠DBC=30°,AB=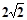 .求BC的长.
.求BC的长.
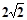 .求BC的长.
.求BC的长.
2.
试题分析:作BE⊥AD于E,就可以得出△ABE为等腰直角三角形,由勾股定理就由求出BE的值,由△BDE≌△BDC就可以得出BC=BE得出结论.
试题解析:作BE⊥AD于E,
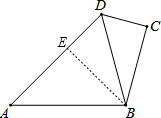
∴∠BEA=∠BED=90°.
∵∠A=45°,
∴∠ABE=45°.
∵∠ABD=75°,
∴∠EBD=30°.
∵∠DBC=30°,
∴∠DBE=∠DBC.
∵∠C=90°,
∴∠BED=∠C.
在△BDE和△BDC中,
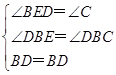 ,
,∴△BDE≌△BDC(AAS),
∴BE=BC.
在Rt△ABE中,AB=2
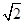 ,由勾股定理,得BE=2
,由勾股定理,得BE=2∴BC=2.
考点: 1.全等三角形的判定与性质;2.角平分线的性质;3.等腰直角三角形.

练习册系列答案
相关题目
 则此三角形的面积为
则此三角形的面积为  .
. 中,
中,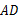 ∥
∥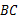 ,
,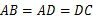 ,
,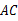 ⊥
⊥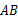 ,延长
,延长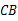 至点
至点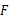 ,使
,使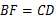 .
.
 的度数.
的度数. 为等腰三角形.
为等腰三角形.

 中,∠
中,∠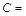 90°,∠
90°,∠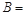 30°,以点
30°,以点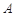 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交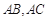 于点
于点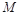 和
和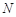 ,再分别以点
,再分别以点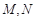 为圆心,大于
为圆心,大于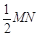 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点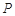 ,连接
,连接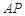 并延长交
并延长交 于点
于点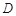 ,则下列说法中正确的个数 是( )
,则下列说法中正确的个数 是( )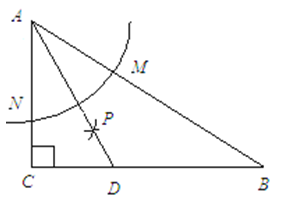
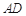 是∠
是∠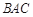 的平分线;②∠
的平分线;②∠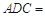 60°;③点
60°;③点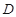 在
在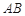 的中垂线上;④
的中垂线上;④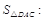
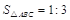 .
.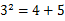
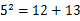
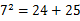
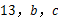
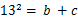
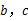 的值.
的值.