Question

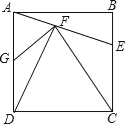
【题目】如图，正方形ABCD中，E为BC中点连接AE，DF⊥AE于点F，连接CF，FG⊥CF交AD于点G，下列结论：①CF=CD；②G为AD中点；③△DCF∽△AGF；④，其中结论正确的个数有（　　）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】D

【解析】

如图，作CM⊥DF于M．首先证明△DAF≌△CDM，推出DM=AF，再证明DF=2AF，推出DM=MF，推出CD=CF，再证明∠GDF=∠GFD，推出GD=GF，再证明GF=GA即可证明GA=GD，由此即可一一判断.

如图，作CM⊥DF于M．

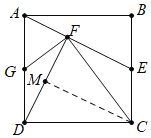
∵四边形ABCD是正方形，

∴AB=BC=CD=AD，∴DAB=∠B=∠ADC=90°，

∵∠ADF+∠CDF=90°，∠CDF+∠DCM=90°，

∴∠ADF=∠DCM，

∵DF⊥AE，CM⊥DF，

∴∠AFD=∠CMD=90°，

∴△DAF≌△CDM，

∴CM=DF，DM=AF，

∵∠ADF+∠DAE=90°，∠DAE+∠BAE=90°，

∴∠BAE=∠ADF，

∵BE=CE，

∴AB=2BE，

∴tan∠BAE=tan∠ADF=，

∴，

∴DM=MF，∵CM⊥DF，

∴CD=CF，故①正确，

∴∠CDF=∠CFD，

∵∠CDG=∠CFG=90°，

∴∠GFD=∠GDF，

∴GF=GD，

∵∠GDF+∠DAF=90°，∠GFD+∠AFG=90°，

∴∠GAF=∠GFA，

∴GF=GA，

∴GD=GA，

∴G是AD中点，故②正确，

∵∠AFD=∠GFC，

∴∠AFG=∠CFD，∠GAF=∠CDF，

∴△DCF∽△AGF，故③正确，

设AF=a，则DF=2a，AB=a，BE=a，

∴AE=a，EF=a，

∴，故④正确，

故选D．