题目内容
【题目】已知△ABC中,∠B= 60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ABE沿DE折叠,点A对应点为F点.
(1)如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;
(2)如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;
(3)如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG的长.
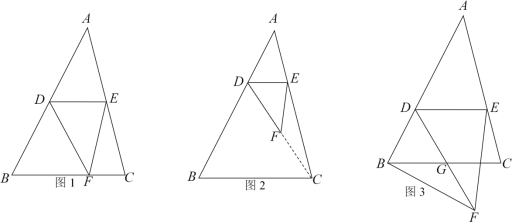
【答案】(1)见解析(2)40°(3)3
【解析】
(1)根据DE∥BC,∠B=60°得到∠ADE=∠B=60°,根据折叠的性质得到∠FDE=∠ADE=60°,从而得到△BDF 是等边三角形
(2)根据CF=EF ,设∠FCE=∠FEC=x,则∠DFE=∠FCE+∠FEC=2x,根据折叠得到∠A=∠DFE=2x ,再由(1)同理可得到△BDC 是等边三角形,再利用△ABC内角和即可列出方程求解
(3)同(1)可得△BDG 是等边三角形,根据BF⊥AB 得到∠BFD=30°,得BD=![]() DF,再根据折叠的性质得到DF=AD,故BD=
DF,再根据折叠的性质得到DF=AD,故BD=![]() AD=
AD=![]() AB=
AB=![]() ×9=3,即可求出BG的长.
×9=3,即可求出BG的长.
(1)证明:∵DE∥BC,∠B=60°
∴∠ADE=∠B=60°
∵△ADE 沿 DE 折叠得到△DEF
∴∠FDE=∠ADE=60°
∴∠BDF=180°-60°-60°=60°
在△BDF 中,∠B=∠BDF=60°
∴△BDF 是等边三角形.
(2)解:∵CF=EF
∴设∠FCE=∠FEC=x,则∠DFE=∠FCE+∠FEC=2x
∵△ADE 沿 DE 折叠得到△DEF
∴∠A=∠DFE=2x
同(1)可得△BDC 是等边三角形
∴∠BCD=60°
在△ABC 中,∠A+∠B+∠BCA=180° ∴2x+60°+(60°+x)=180° 解得:x=20°
∴∠A=2x=40°.
(3)解:同(1)可得△BDG 是等边三角形
∴∠BDG=60°,BG=BD
∵BF⊥AB
∴∠DBF=90°
∴∠BFD=90°-60°=30°
∴BD=![]() DF
DF
又∵△ADE 沿 DE 折叠得到△DEF
∴DF=AD
∴BD=![]() AD=
AD=![]() AB=
AB=![]() ×9=3
×9=3
∴BG=3.