Question

【题目】如图，正方形AOBC的两边在坐标轴上，D是OB的中点，直线CD的函数关系式为y=2x﹣6，则△CDE的面积为 ． （平方单位）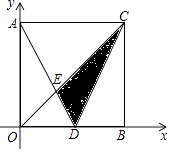

Answer 1

【答案】6
【解析】解：在y=2x﹣6中，令y=0时，x=3，即D（3，0）， ∴OD=BD=3，
又∵D是OB的中点，
∴OB=OA=6，
即A（0，6），C（6，6），
由A（0，6），D（3，0）可得直线AD的解析式是y=﹣2x+6，
由C（6，6）可得直线OC解析式为y=x，
解方程组 ，可得 ，
∴E（2，2），
∴点E离AC的距离为4，
∴△CDE的面积=△ACD的面积﹣△ACE的面积= ×6×6﹣ ×6×4=6．
所以答案是：6．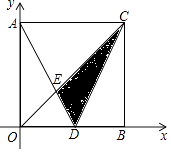

【考点精析】本题主要考查了正方形的性质的相关知识点，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题．